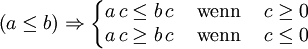Monotoniekriterium

In der Mathematik heißt eine Funktion oder Folge, die nur größer wird oder konstant ist (und niemals fällt), monoton steigend (oder monoton wachsend bzw. isoton). Entsprechend heißt eine Funktion oder Folge monoton fallend (antiton), wenn sie nur kleiner wird oder konstant bleibt. Ändern sich die Werte der Funktion oder die Glieder der Folge nicht, heißt sie konstant.

Streng monoton steigend (bzw. streng monoton fallend) sind Funktionen oder Folgen, die nur größer (kleiner) werden, aber nicht konstant sind.

Beispiele

Die Funktion y=x³ ist überall streng monoton steigend.

Die Folge

1,3,5,7,9,11,...

ist streng monoton steigend.

Die Folge

1,3,3,5,6,8,8,9,1000,1200

ist monoton steigend, jedoch nicht streng monoton steigend (3 und 8 kommen doppelt vor).

Die Folge

2,2,2,2,2,2,2,...

ist konstant.

Die Funktion

y = x³

ist über den gesamten Wertebereich streng monoton steigend. Bei x=0 hat sie zwar eine Steigung von 0, jedoch nur an diesem einen Punkt.

Die Funktion

y = x²

ist im Bereich von minus unendlich bis Null (einschließlich) $(x \leq 0)$ streng monoton fallend. Im Bereich von Null (einschließlich) bis plus unendlich $(x \geq 0)$ ist sie streng monoton steigend.

Definitionen

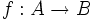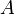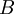Sei $\begin{matrix}f: A \rightarrow B\end{matrix}$ eine Funktion. Auf $\begin{matrix} A \end{matrix}$ und $\begin{matrix} B \end{matrix}$ sei jeweils eine Ordnungsrelation 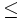$\begin{matrix} \leq \end{matrix}$ definiert. Dann heißt die Funktion 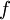$\begin{matrix} f \end{matrix}$ monoton steigend, wenn:

für alle $a,b \in A: a < b \Rightarrow f(a) \leq f(b)$.

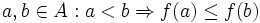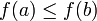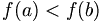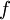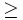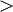Gilt anstelle von $f(a) \leq f(b)$ sogar $\begin{matrix}f(a) < f(b) \end{matrix}$, so heißt die Funktion $\begin{matrix} f \end{matrix}$ streng monoton steigend. Entsprechend gilt natürlich für $\begin{matrix} \geq \end{matrix}$ bzw. $\begin{matrix} > \end{matrix}$ monoton fallend bzw. streng monoton fallend.

Eine Folge 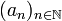$(a_{n})_{n \in \mathbb{N}}$ heißt monoton steigend, wenn für alle $n \in \mathbb{N}$ gilt: $a_{n+1} \geq a_n$.

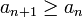Eine Folge 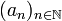$(a_{n})_{n \in \mathbb{N}}$ heißt streng monoton steigend, wenn für alle $n \in \mathbb{N}$ gilt: $\begin{matrix}a_{n+1} > a_n\end{matrix}$.

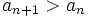Weitere Eigenschaften

Für eine reelle monotone Funktion f gilt:

• Sie hat in jedem Häufungspunkt ihres Definitionsbereichs einen linksseitigen und rechtsseitigen Grenzwert.
• Sie kann nur Sprungstellen als Unstetigkeitsstellen haben.
• Die Menge der Sprungstellen in ihrem Definitionsbereich ist abzählbar, muss aber nicht notwendigerweise endlich sein.
• Sie ist fast überall differenzierbar, d. h. die Menge der Stellen, an denen f nicht differenzierbar ist, bildet eine lebesguesche Nullmenge.
• Eine im Intervall [a, b] definierte monotone Funktion ist dort Riemann-integrierbar.

Monotonie differenzierbarer reeller Funktionen

• Eine stetig differenzierbare Funktion auf einem Intervall ist genau dann monoton wachsend (bzw. monoton fallend), wenn die Ableitung nirgendwo negativ (bzw. nirgendwo positiv) ist.
• Eine stetig differenzierbare Funktion auf einem Intervall ist genau dann streng monoton wachsend (bzw. streng monoton fallend), wenn die Ableitung
  • nirgendwo negativ (bzw. nirgendwo positiv) und
  • auf keinem echtem Teilintervall konstant gleich null ist (wobei ein echtes Intervall ein Intervall mit mehr als einem Element ist).

Umkehrfunktion

Sei 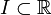$I\subset\mathbb{R}$ ein Intervall und 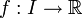$f:I\rightarrow\mathbb{R}$ sei streng monoton wachsend/fallend und stetig. Dann ist

• die Bildmenge 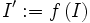$I':= f\left(I\right)$ ein Intervall
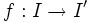• $f:I\rightarrow I'$ bijektiv
• die Umkehrfunktion 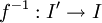$f^{-1}:I'\rightarrow I$ streng monoton wachsend/fallend und stetig
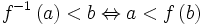• $f^{-1}\left(a\right)<b\Leftrightarrow a<f\left(b\right)$ wenn wachsend und
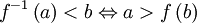• $f^{-1}\left(a\right)<b\Leftrightarrow a>f\left(b\right)$ wenn fallend

Monotoniegesetze

Für 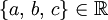$\left\{ a,\,b,\,c \right\} \in \mathbb{R}$ gilt:

1. $\left( a \le b \right) \Rightarrow \left[ \left( a + c \right) \le \left( b + c \right) \right]$
2. $\left( a \le b \right) \Rightarrow \left\{ \begin{matrix}{a\,c \le b\,c} & \text{ wenn } & {c \ge 0} \\ {a\,c \ge b\,c} & \text{ wenn } & {c \le 0} \end{matrix} \right.$

Weblinks

• Monotonie von Funktionen (Das Verhalten der Funktion im Vergleich zur Ableitungsfunktion)
• Die Umkehrfunktion einer stetigen, streng monotonen Funktion