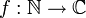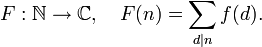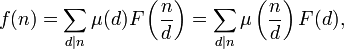Inzidenzalgebra — Die Inzidenzalgebra einer Halbordnung wurde 1964 von Gian Carlo Rota zur Untersuchung kombinatorischer Sachverhalte eingeführt. Inhaltsverzeichnis 1 Formale Definition 2 Eigenschaften 3 Verallgemeinerte Möbiussche Umkehrformel … Deutsch Wikipedia
Arithmetische Funktion — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
Dirichlet-Faltung — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
Multiplikative Funktion — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
Multiplikativität — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
Summatorische Funktion — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
Möbius-Inversion — Die Möbiussche Umkehrformel geht auf August Ferdinand Möbius zurück und erlaubt es, eine zahlentheoretische Funktion aus ihrer summatorischen Funktion zu rekonstruieren. Gegeben seien eine zahlentheoretische Funktion und ihre summatorische… … Deutsch Wikipedia
Zahlentheoretische Funktion — Eine zahlentheoretische oder arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von natürlichen… … Deutsch Wikipedia