- Möndchen
-
Mit den Möndchen des Hippokrates, die dem griechischen Mathematiker Hippokrates von Chios (um 450 v. Chr.) zugeschrieben werden, konnte man bereits im vorchristlichen Griechenland nachweisen, dass auch krummlinig begrenzte Flächenstücke durch rationale Zahlen berechnet werden können.
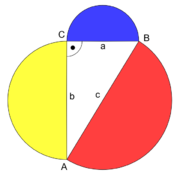
Nach dem Satz des Pythagoras ist die Summe der Flächen der Kathetenquadrate eines rechtwinkligen Dreiecks gleich der Fläche des Hypotenusenquadrats. Nach dem verallgemeinerten Satz des Pythagoras gilt dieser Zusammenhang auch für andere ähnliche Figuren. Für Halbkreise bedeutet das: die Flächensumme der Halbkreise über den Katheten entspricht der Fläche des Halbkreises über der Hypotenuse (Schritt 1).
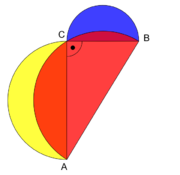
Spiegelt man den Halbkreis über der Hypotenuse, so überlappt dieser mit den beiden Kathetenhalbkreisen (Schritt 2). Entfernt man die überlappenden Kreissegmente (Schritt 3), verbleiben vom Hypotenusenhalbkreis das Dreieck selbst und von den beiden Kathetenhalbkreisen die beiden sichelförmigen äußeren Kreisteile, die Möndchen.
Es gilt also:
Varianten
Es gibt die verschiedensten Varianten und Möglichkeiten der Verallgemeinerung des Satzes von Pythagoras und der Möndchen des Hippokrates. Neben dem bereits genannten rechtwinkligen Dreieck ist das folgende Quadrat, über dessen vier Quadratseiten jeweils ein Möndchen ist, ein weiteres Beispiel.
Literatur
- Egmont Colerus: Vom Einmaleins zum Integral. Mathematik für Jedermann. Rowohlt, Reinbek 1982, (Kapitel Problem der Quadratur, S. 249 in Ausgabe Paul Szolnay Verlag, 1934) ISBN 3-499-16692-5
- Paul Karlson: Vom Zauber der Zahlen. Eine unterhaltsame Mathematik für Jedermann. Ullstein, Berlin 1954, S. 140
- Hans Wußing: 6000 Jahre Mathematik. Springer, Berlin u. a. 2008, ISBN 978-3-540-77189-0, S. 172ff
Weblinks
Wikimedia Foundation.

.jpg)


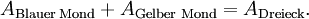
.jpg)