- Ähnlichkeit (Geometrie)
-
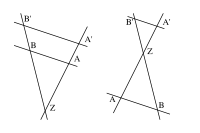
In der Geometrie sind zwei Figuren genau dann zu einander ähnlich, wenn sie durch eine Ähnlichkeitsabbildung (auch diese Abbildung wird häufig als Ähnlichkeit bezeichnet), das heißt eine geometrische Abbildung, die sich aus zentrischen Streckungen und Kongruenzabbildungen - Verschiebung, Drehung, Spiegelung - zusammensetzen lässt, ineinander überführt werden können. Ähnlichkeit erweitert somit die Kongruenz um die Möglichkeit der Streckung.
Inhaltsverzeichnis
Eigenschaften
Winkel und Streckenverhältnisse stimmen in ähnlichen Figuren überein; somit sind alle Kreise sowie jeweils alle regelmäßigen Polygone gleichen Grades, wie gleichseitige Dreiecke und Quadrate, zueinander ähnlich.
Es gilt, dass kongruente Figuren stets ähnlich sind. Das Umgekehrte ist hingegen falsch: Ähnliche Figuren sind nicht notwendigerweise kongruent, da sie verschieden groß sein können.
Als mathematisches Zeichen für geometrische Ähnlichkeit wird ∼ (die Tilde) verwendet, z.B:
 bedeutet, dass die Dreiecke ΔABC und ΔA'B'C' ähnlich sind. Will man dagegen Kongruenz ausdrücken, so kann stattdessen
bedeutet, dass die Dreiecke ΔABC und ΔA'B'C' ähnlich sind. Will man dagegen Kongruenz ausdrücken, so kann stattdessen  oder
oder  (eine "Mischung" mit dem Gleichheitszeichen) verwendet werden.
(eine "Mischung" mit dem Gleichheitszeichen) verwendet werden.Ähnlichkeit bei Dreiecken
Dreiecke spielen hier eine zentrale Rolle, da sich sehr viele Figuren auf solche zurückführen lassen. Es gilt:
Zwei Dreiecke sind zueinander ähnlich, wenn
- sie in zwei (und somit in allen drei) Winkeln übereinstimmen; oder
- sie in allen Verhältnissen entsprechender Seiten übereinstimmen; oder
- sie in einem Winkel und im Verhältnis der anliegenden Seiten übereinstimmen; oder
- sie im Verhältnis zweier Seiten und im Gegenwinkel der größeren Seite übereinstimmen.
Diese Sätze werden Ähnlichkeitssätze genannt.
Strahlensätze
Die Strahlensätze machen über die Verhältnisse der Dreiecksseiten bestimmter ähnlicher Dreiecke wichtige Aussagen.
Ähnlichkeit in der fraktalen Geometrie
Skaleninvariante Ähnlichkeit in gebrochenen, „fraktalen“ Dimensionen ist Gegenstand der fraktalen Geometrie.
Die Ähnlichkeit ist dabei das Ergebnis der Rekursion nichtlinearer Algorithmen. Ein bekanntes Beispiel ist die Mandelbrot-Menge, deren Grenzlinie an jeder Stelle Ähnlichkeit mit den angrenzenden Abschnitten in allen Größenordnungen aufweist.
Kategorie:- Geometrische Abbildung
Wikimedia Foundation.