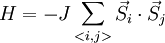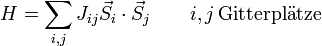N-Vektor-Modell

Das n-Vektor-Modell oder auch O(n)-Modell ist ein Modell der statistischen Physik. Es handelt sich dabei um ein stark vereinfachtes Modell (oder effektives Modell) zur Beschreibung von Phasenübergangen, kritischem Verhalten und Magnetismus. Im Modell sind (klassische) Spins mit n-Komponenten auf den Gitterpunkten eines Kristallgitters platziert. In der ursprünglichen Formulierung^[1] des Modells von H. E. Stanley aus dem Jahre 1968 wechselwirken dabei lediglich die am nächstbenachbarten Spins miteinander (nächste Nachbarwechselwirkung) und die Spins besitzen Einheitslänge. Der Hamiltonian ist gegeben als:

$H = -J\sum_{<i,j>}\vec{S}_i \cdot \vec{S}_j$

Die Summe läuft über alle Paare von benachbarten Spins. Es sei darauf hingewiesen, dass die Spins die Dimension n besitzen, dass Kristallgitter aber eine davon unterschiedliche Dimension d besitzen kann. Das n-Vektor-Modell enthält als Spezialfälle folgende intensiv untersuchte Modelle in der statistischen Physik:

n = 0 || Self-Avoiding Walks (SAW)

n = 1 || Das Ising-Modell

n = 2 || Das (klassische) XY-Modell

n = 3 || Das (klassische) Heisenberg-Modell

Die Diskussion des Modells geschieht am Besten in den verschiedenen Spezialfällen.

Verallgemeinerungen des Modells

Eine übliche Verallgemeinerung des Modells in allen Spezialfällen ist nicht nur nächste Nachbarwechselwirkung zu betrachten, sondern auch weiter entfernte Nachbarwechselwirkungen zu untersuchen. Dabei kann auch die Kopplungskonstante vom Ort abhängen. Der Hamiltonian ist dann gegeben als:

$H = \sum_{i,j}J_{ij}\vec{S}_i \cdot \vec{S}_j\qquad i, j \,\mathrm{Gitterpl\ddot atze}$

Weitere Verallgemeinerungen sind in den jeweiligen Spezialfällen angegeben.

Quantenmechanische Formulierung

In der quantenmechanischen Formulierung betrachtet man nicht mehr klassische Spins sondern quantenmechanische Spins ausgedrückt über Spinoperatoren. Einer der Hauptunterschiede besteht darin, dass die Spinoperatoren in verschiedenen Dimensionen n nicht mehr vertauschen (kommutieren). Die Spezialfälle des n-Vektor-Modells sind dann:

n = 0 || Self-Avoiding Walks (SAW)

n = 1 || Das Ising-Modell

n = 2 || Das (quantenmechanische) XY-Modell

n = 3 || Das (quantenmechanische) Heisenberg-Modell

Quellen

1. ↑ H. E. Stanley, Phys. Rev. Lett. 20,589 (1968); Phys Rev. 176, 718 (1968)