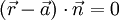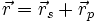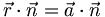Normalengleichung einer Ebene
- Normalengleichung einer Ebene
-
Die Normalgleichung (oder auch Normalengleichung) einer Ebene hat die Form
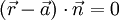
oder
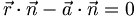
wobei  ein Normalenvektor der Ebene,
ein Normalenvektor der Ebene,  der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und
der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und 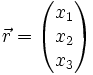 der Vektor der Unbekannten ist. Der Operator
der Vektor der Unbekannten ist. Der Operator  steht für das Skalarprodukt.
steht für das Skalarprodukt.
Jeder Punkt, dessen Ortsvektor 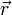 die Gleichung erfüllt, liegt in der Ebene.
die Gleichung erfüllt, liegt in der Ebene.
Ein Punkt, dessen Ortsvektor  die Normalgleichung nicht erfüllt, liegt (bezogen auf die Richtung des Normalenvektors)
die Normalgleichung nicht erfüllt, liegt (bezogen auf die Richtung des Normalenvektors)
- vor der Ebene, wenn
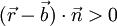
- hinter der Ebene, wenn
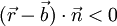 .
.
Erklärung
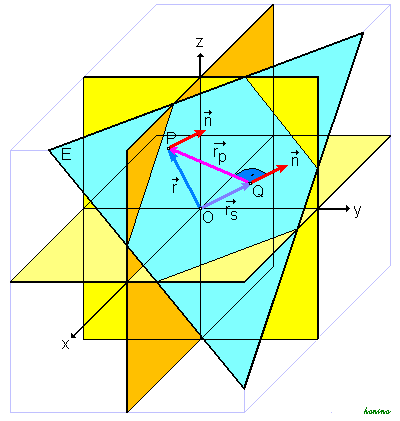
Der Ortsvektor 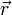 eines beliebigen Punktes P der Ebene lässt sich als Summe
eines beliebigen Punktes P der Ebene lässt sich als Summe
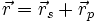
darstellen, wobei 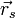 senkrecht zur Ebene (also parallel zu
senkrecht zur Ebene (also parallel zu  ) und
) und 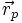 parallel zur Ebene (also senkrecht zu
parallel zur Ebene (also senkrecht zu  ) verläuft.
) verläuft.
Dann ist
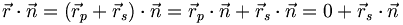 ,
,
weil 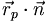 (als Skalarprodukt zueinander senkrechter Vektoren) stets 0 ist. Der Anteil
(als Skalarprodukt zueinander senkrechter Vektoren) stets 0 ist. Der Anteil 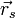 ist aber für jeden in der Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Ebene
ist aber für jeden in der Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Ebene 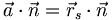 konstant. Damit folgt die Normalform
konstant. Damit folgt die Normalform
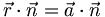
oder
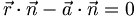 .
.
Siehe auch: Hessesche Normalform, Geradengleichung
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Normalgleichung einer Ebene — Die Normalgleichung (oder auch Normalengleichung) einer Ebene hat die Form oder wobei ein Normalenvektor der Ebene, der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und … Deutsch Wikipedia
Normalengleichung — Die Normalgleichung (oder auch Normalengleichung) einer Ebene hat die Form oder wobei ein Normalenvektor der Ebene, der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und … Deutsch Wikipedia
Hessesche Normalengleichung — Darstellung von Normale und Abstand der hesseschen Normalform Die hessesche Normalform (Hesse Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum oder eine … Deutsch Wikipedia
Normalenform — Die Normalgleichung (oder auch Normalengleichung) einer Ebene hat die Form oder wobei ein Normalenvektor der Ebene, der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und … Deutsch Wikipedia
Normalgleichung — Die Normalgleichung (oder auch Normalengleichung) einer Ebene hat die Form oder wobei ein Normalenvektor der Ebene, der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und … Deutsch Wikipedia
Formelsammlung Analytische Geometrie — Dieser Artikel ist eine Formelsammlung zum Thema Analytische Geometrie. Es werden mathematische Symbole verwendet, die im Artikel Mathematische Symbole erläutert werden. Dies ist eine Formelsammlung zu dem mathematischen Teilgebiet Analytische… … Deutsch Wikipedia
Direktrix — In der ebenen Geometrie versteht man unter einer Ellipse eine spezielle geschlossene, glatte Kurve, das gestreckte oder gestauchte Bild eines Kreises. Die Ellipse gehört ebenso wie der Kreis, die Parabel und die Hyperbel zu den Kegelschnitten.… … Deutsch Wikipedia
Ellipse — geometrisch Die Saturnringe erscheinen elliptisch … Deutsch Wikipedia
Ellipse (Geometrie) — In der ebenen Geometrie versteht man unter einer Ellipse eine spezielle geschlossene, glatte Kurve, das gestreckte oder gestauchte Bild eines Kreises. Die Ellipse gehört ebenso wie der Kreis, die Parabel und die Hyperbel zu den Kegelschnitten.… … Deutsch Wikipedia
Ellipsenzirkel — In der ebenen Geometrie versteht man unter einer Ellipse eine spezielle geschlossene, glatte Kurve, das gestreckte oder gestauchte Bild eines Kreises. Die Ellipse gehört ebenso wie der Kreis, die Parabel und die Hyperbel zu den Kegelschnitten.… … Deutsch Wikipedia
 ein Normalenvektor der Ebene,
ein Normalenvektor der Ebene,  der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und
der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und 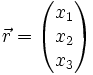 der Vektor der Unbekannten ist. Der Operator
der Vektor der Unbekannten ist. Der Operator  steht für das Skalarprodukt.
steht für das Skalarprodukt. die Gleichung erfüllt, liegt in der Ebene.
die Gleichung erfüllt, liegt in der Ebene. die Normalgleichung nicht erfüllt, liegt (bezogen auf die Richtung des Normalenvektors)
die Normalgleichung nicht erfüllt, liegt (bezogen auf die Richtung des Normalenvektors)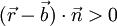
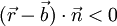 .
.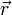 eines beliebigen Punktes P der Ebene lässt sich als Summe
eines beliebigen Punktes P der Ebene lässt sich als Summe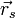 senkrecht zur Ebene (also parallel zu
senkrecht zur Ebene (also parallel zu  ) und
) und 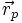 parallel zur Ebene (also senkrecht zu
parallel zur Ebene (also senkrecht zu  ) verläuft.
) verläuft.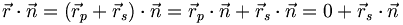 ,
,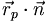 (als Skalarprodukt zueinander senkrechter Vektoren) stets 0 ist. Der Anteil
(als Skalarprodukt zueinander senkrechter Vektoren) stets 0 ist. Der Anteil 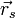 ist aber für jeden in der Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Ebene
ist aber für jeden in der Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Ebene 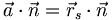 konstant. Damit folgt die Normalform
konstant. Damit folgt die Normalform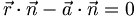 .
.