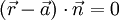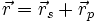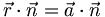Normalgleichung einer Ebene
- Normalgleichung einer Ebene
-
Die Normalgleichung (oder auch Normalengleichung) einer Ebene hat die Form
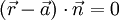
oder
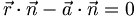
wobei  ein Normalenvektor der Ebene,
ein Normalenvektor der Ebene,  der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und
der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und 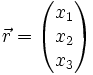 der Vektor der Unbekannten ist. Der Operator
der Vektor der Unbekannten ist. Der Operator  steht für das Skalarprodukt.
steht für das Skalarprodukt.
Jeder Punkt, dessen Ortsvektor 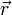 die Gleichung erfüllt, liegt in der Ebene.
die Gleichung erfüllt, liegt in der Ebene.
Ein Punkt, dessen Ortsvektor  die Normalgleichung nicht erfüllt, liegt (bezogen auf die Richtung des Normalenvektors)
die Normalgleichung nicht erfüllt, liegt (bezogen auf die Richtung des Normalenvektors)
- vor der Ebene, wenn
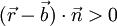
- hinter der Ebene, wenn
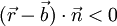 .
.
Erklärung
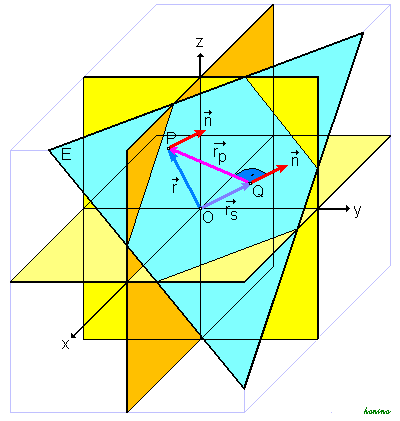
Der Ortsvektor 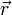 eines beliebigen Punktes P der Ebene lässt sich als Summe
eines beliebigen Punktes P der Ebene lässt sich als Summe
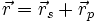
darstellen, wobei 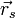 senkrecht zur Ebene (also parallel zu
senkrecht zur Ebene (also parallel zu  ) und
) und 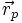 parallel zur Ebene (also senkrecht zu
parallel zur Ebene (also senkrecht zu  ) verläuft.
) verläuft.
Dann ist
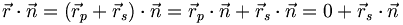 ,
,
weil 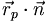 (als Skalarprodukt zueinander senkrechter Vektoren) stets 0 ist. Der Anteil
(als Skalarprodukt zueinander senkrechter Vektoren) stets 0 ist. Der Anteil 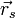 ist aber für jeden in der Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Ebene
ist aber für jeden in der Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Ebene 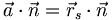 konstant. Damit folgt die Normalform
konstant. Damit folgt die Normalform
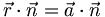
oder
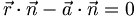 .
.
Siehe auch: Hessesche Normalform, Geradengleichung
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Normalengleichung einer Ebene — Die Normalgleichung (oder auch Normalengleichung) einer Ebene hat die Form oder wobei ein Normalenvektor der Ebene, der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und … Deutsch Wikipedia
Normalgleichung — Die Normalgleichung (oder auch Normalengleichung) einer Ebene hat die Form oder wobei ein Normalenvektor der Ebene, der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und … Deutsch Wikipedia
Ebene (Mathematik) — Die 3 Koordinatenebenen Die Ebene ist ein Grundbegriff der Geometrie. Allgemein handelt es sich um ein unbegrenzt ausgedehntes flaches zweidimensionales Objekt. Hierbei bedeutet unbegrenzt ausgedehnt und flach, dass zu je zwei Punkten auch eine… … Deutsch Wikipedia
Hesse'sche Normalenform — Darstellung von Normale und Abstand der hesseschen Normalform Die hessesche Normalform (Hesse Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum oder eine … Deutsch Wikipedia
Hesse'sche Normalform — Darstellung von Normale und Abstand der hesseschen Normalform Die hessesche Normalform (Hesse Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum oder eine … Deutsch Wikipedia
Hesse-Normalenform — Darstellung von Normale und Abstand der hesseschen Normalform Die hessesche Normalform (Hesse Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum oder eine … Deutsch Wikipedia
Hesse-Normalform — Darstellung von Normale und Abstand der hesseschen Normalform Die hessesche Normalform (Hesse Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum oder eine … Deutsch Wikipedia
Hesseform — Darstellung von Normale und Abstand der hesseschen Normalform Die hessesche Normalform (Hesse Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum oder eine … Deutsch Wikipedia
Hessesche Normalenform — Darstellung von Normale und Abstand der hesseschen Normalform Die hessesche Normalform (Hesse Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum oder eine … Deutsch Wikipedia
Hessesche Normalengleichung — Darstellung von Normale und Abstand der hesseschen Normalform Die hessesche Normalform (Hesse Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum oder eine … Deutsch Wikipedia
 ein Normalenvektor der Ebene,
ein Normalenvektor der Ebene,  der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und
der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und 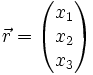 der Vektor der Unbekannten ist. Der Operator
der Vektor der Unbekannten ist. Der Operator  steht für das Skalarprodukt.
steht für das Skalarprodukt.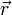 die Gleichung erfüllt, liegt in der Ebene.
die Gleichung erfüllt, liegt in der Ebene. die Normalgleichung nicht erfüllt, liegt (bezogen auf die Richtung des Normalenvektors)
die Normalgleichung nicht erfüllt, liegt (bezogen auf die Richtung des Normalenvektors)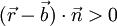
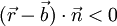 .
.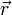 eines beliebigen Punktes P der Ebene lässt sich als Summe
eines beliebigen Punktes P der Ebene lässt sich als Summe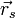 senkrecht zur Ebene (also parallel zu
senkrecht zur Ebene (also parallel zu  ) und
) und 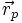 parallel zur Ebene (also senkrecht zu
parallel zur Ebene (also senkrecht zu  ) verläuft.
) verläuft.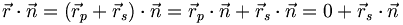 ,
,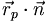 (als Skalarprodukt zueinander senkrechter Vektoren) stets 0 ist. Der Anteil
(als Skalarprodukt zueinander senkrechter Vektoren) stets 0 ist. Der Anteil 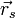 ist aber für jeden in der Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Ebene
ist aber für jeden in der Ebene liegenden Punkt der gleiche, also ist für jeden Punkt der Ebene 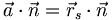 konstant. Damit folgt die Normalform
konstant. Damit folgt die Normalform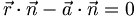 .
.