Null-Eins-Gesetz von Kolmogoroff

Als Null-Eins-Gesetze werden in der Wahrscheinlichkeitstheorie solche Sätze bezeichnet, die besagen, dass die Wahrscheinlichkeit für Ereignisse eines bestimmten Typs entweder 0 oder 1 sind. Das heißt: Sie treten entweder sicher ein oder sicher nicht.

Null-Eins-Gesetz von Kolmogorow

Das wohl bekannteste Null-Eins-Gesetz stammt von Andrei Kolmogorow und lässt sich wie folgt formulieren:

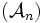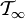Für eine Folge stochastisch unabhängiger σ-Algebren $(\mathcal A_n)$ sei $\mathcal T_{\infty}$ die terminale σ-Algebra. Dann gilt für jedes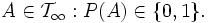 $A \in \mathcal T_{\infty}: P(A) \in \{0,1\}.$

Der Beweis fußt darauf, dass sich aus elementaren Umformungen der Unabhängigkeitseigenschaft der σ-Algebren zeigen lässt, dass 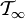$\mathcal T_{\infty}$ unabhängig zu sich selbst ist, mithin also 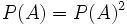$P(A) = P(A)^2\;$ gelten muss.

Null-Eins-Gesetz von Borel

Das Émile Borel zugeschriebene Null-Eins-Gesetz besagt als Folgerung aus dem Kolmogorowschen Gesetz, dass die Wahrscheinlichkeit für den Limes superior einer Folge unabhängiger Ereignisse immer entweder 0 oder 1 ist.

Diese Aussage ist eng mit dem Borel-Cantelli-Lemma verbunden.