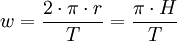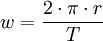Orbitalgeschwindigkeit (Wasserwellen)

Trochoidale Tiefwasserwelle: Momentane Richtungen der Orbitalgeschwindigkeit $w =\frac{2\cdot \pi \cdot r}{T} =\frac{ \pi \cdot H}{T}$ an verschiedenen Positionen der Wellenoberfläche.

Tiefwasserwelle nach Stokes: Orbitalbahnen der Wasserteilchen beginnend an zwei Positionen mit dem Abstand einer halben Wellenlänge.

Flachwasserwelle nach Stokes: Orbitalbahnen der Wasserteilchen beginnend an zwei Positionen mit dem Abstand einer halben Wellenlänge.

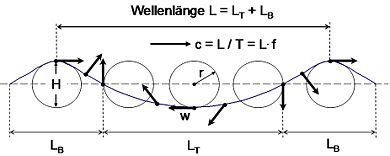
Unter Orbitalbewegung (von lateinisch orbis, Kreis) wird bei Wasserwellen die Bewegung der Wasserteilchen verstanden. In tiefem Wasser sind die Bahnen der Wasserteilchen beim Passieren einer Welle nahezu kreisförmig und in flachem Wasser nahezu elliptisch. Die Abweichung von der exakt kreisförmigen bzw. exakt elliptischen Bahnform ist auf eine überlagerte Driftgeschwindigkeit zurückzuführen, die der Wellenfortschrittsgeschwindigkeit c gleichgerichtet ist und Massentransportgeschwindigkeit U genannt wird. Letztere ist viel kleiner als c, wächst mit zunehmender Wellensteilheit S = H/L (H = Wellenhöhe, L = Wellenlänge) und bewirkt die Ausbildung spiralförmiger Orbitalbahnen, vergl. nebenstehende Animationen.

Teilchenbewegung im Wellenfeld

In der Praxis verwendete Wellentheorien gehen davon aus, dass jegliche Orbitalbewegung in einer Tiefe, die etwa der halben Wellenlänge L entspricht, vernachlässigbar gering ist und eine wellenerzeugte Durchmischung - im Gegensatz zu den Wirkungen anderer Strömungen - unterhalb dieser Marke nicht mehr stattfindet. Als Näherung wird die Abnahme der Bewegungsamplituden mit zunehmender Entfernung von der Wasseroberfläche nach einem Exponentialgesetz angenommen.
Häufig ist es ausreichend, den Massentransport unberücksichtigt zu lassen; insbesondere für Wellen über großer Wassertiefe (Tiefwasserwellen), für die die Trochoidaltheorie nach Gerstner befriedigende Ergebnisse sowohl für die kreisförmige Wasserteilchenkinematik als auch für die Oberflächenkontur liefert, vergl. Bild oben. Die Wellenperiode T (= 1/f; Kehrwert der Frequenz f) ist die Umlaufzeit, die dem Vorrücken der Welle um eine volle Wellenlänge L entspricht. Somit ist die Orbitalgeschwindigkeit an der Wasseroberfläche

$w = \frac{2\cdot \pi \cdot r}{T}$

und die Wellenfortschrittsgeschwindigkeit

$c = \frac{L}{T}$.

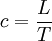Bei periodischen Wellen, die in Bereiche abnehmender Wassertiefe hineinlaufen, verändern sich die vorher kreisförmigen Bahnen zu offenen Ellipsen bis die Orbitalbewegung im Verlauf des Wellenbrechens ihren zirkularen Charakter dadurch verliert, dass ihre horizontale Komponente auf Kosten der vertikale Komponente anwächst. Nach dem Brechvorgang (hier noch nicht bildlich dargestellt) ist die Wellenbewegung aperiodisch; die Bewegung der einzelnen Wasserteilchen erstreckt sich über die gesamte Wassertiefe etwa gleichermaßen horizontal in küstenwärtiger Richtung.

Technische Bedeutung

Für praktische Anwendungen wird die resultierende Orbitalgeschwindigkeit in zwei senkrecht zueinander stehende Komponenten zerlegt. Da an einer festen Begrenzung keine Geschwindigkeitskomponenten senkrecht dazu möglich sind, kommt es hier etwa zu einer Verdoppelung der tangentialen Komponente. Dementsprechend ist die Amplitude der horizontalen Schwingung der Wasserteilchen am Boden etwa doppelt so groß wie die Amplitude, die in derselben Tiefe vorliegen würde, wenn der Boden nicht vorhanden wäre. Dieser Sachverhalt ist von besonderer Bedeutung, weil durch wellenerzeugte Sohlströmungen der Sedimenttransport bewirkt wird.
Ähnliches gilt für die Verdoppelung der vertikalen Schwingungsamplitude der Wasserteilchen an einer vertikalen Wand, wo es zur Ausbildung einer stehenden Welle (Clapotis) kommt.
Zur Abschätzung der Wellenkräfte, die auf getauchte Bauwerksstrukturen (z. B. Pfahlbauwerke, Unterwasser-Pipelines) ausgeübt werden, wird in den betreffenden Kraftansätzen neben der örtlichen Orbitalgeschwindigkeit u auch die Orbitalbeschleunigung du/dt verwendet.

Geschichte

Die Trochoidale Wellentheorie wurde 1804 von Franz Josef von Gerstner entwickelt und ist als Grundlage aller folgenden Wellentheorien anzusehen, da sie bereits die Abnahme von Orbitalbahnradien zum Meeresboden hin enthält. Gerstner war dabei von der Rotation der Wasserteilchen um Orbitalzentren ausgegangen und erhielt daraus für die Wasseroberfläche die Form einer zyklischen Kurve. Ebenfalls von den Bahnlinien der Wasserteilchen ausgehend oder unter Verwendung des Geschwindigkeitspotentials sind alle anderen heute bekannten Näherungslösungen entstanden. Bevorzugte Verwendung findet die Lineare Wellentheorie nach Airy-Laplace (1845), der als Wellenform eine Kosinusfuktion zugrunde liegt und die keinen Massentransport beinhaltet. Im Gegensatz dazu stehen die Wellentheorien höherer Ordnung nach Stokes (1880). Für Flachwasserwellen wurde von Korteweg und De Vries (1895) die Cnoidaltheorie entwickelt und für sehr flaches Wasser nahe der Brecherzone von Munk (1949) die Einzelwellentheorie verwendet.

Weblinks

• Trochoidale Wellentheorie in „Energie regulärer Wellen“, Universität Leipzig, Abs.: 4.2.3.4, PDF
• Orbitalbahnen und Orbitalgeschwindigkeiten, PDF

Literatur

• Büsching, F.: Über Orbitalgeschwindigkeiten irregulärer Brandungswellen., Mitt. des Leichtweiß-Instituts der TU Braunschweig, H.42, 1974