PARTITION

Das Partitionsproblem (auch Zahlenaufteilungsproblem, oft mit PARTITION notiert) ist ein Optimierungs- bzw. Entscheidungsproblem der Kombinatorik.

Formulierung des Partitionsproblems

Die Aufgabenstellung beim Partitionsproblem lautet: Gegeben sei eine (Multi-)Menge von (positiven) Zahlen. Gesucht wird eine Aufteilung dieser Zahlen auf zwei Haufen, so dass die Differenz der Summen der Zahlen in den beiden Haufen möglichst klein ist.

Eine äquivalente Formulierung lautet präziser: Gegeben sei eine (Multi-)Menge A von N positiven Zahlen a_i. Gesucht wird eine Untermenge 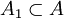$A_1 \subset A$, so dass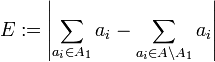

$E := \left| \sum_{a_i \in A_1} a_i - \sum_{a_i \in A \setminus A_1} a_i \right|$

minimal wird. Ist die Summe aller N Zahlen ungerade, so ist die minimale Differenz E_min eins, ansonsten null. Eine Aufteilung, für die E = E_min ist, heißt perfekte Aufteilung.

Als zusätzliche Bedingung kann man die Lösungsmenge des Partitionsproblems von vornherein einschränken, indem man nur ausgewogene Aufteilungen zulässt, in denen beide Haufen gleich groß sind, das heißt die Anzahl der Zahlen in den Untermengen muss für gerades N gleich sein und muss sich für ungerades N um 1 unterscheiden.

Wandelt man die Fragestellung ab und fragt, „Gibt es eine perfekte Aufteilung?“ oder „Existiert eine Aufteilung, für die E maximal ... ist?“, so wird das oben beschriebene Optimierungsproblem zu einem Entscheidungsproblem, das heißt, man sucht nicht mehr nach der besten Aufteilung, sondern fragt nur noch nach deren Existenz.

Phasenübergang im Partitionsproblem

Man beobachtet beim Partitionsproblem zwei verschiedene sogenannte Phasen: Besteht die Menge A aus vielen kleinen Zahlen, so ist anschaulich klar, dass es viele perfekte Aufteilungen gibt, und es einfach ist, eine dieser Aufteilungen zu finden (einfache Phase). Besteht A hingegen aus wenigen großen Zahlen, so ist es unwahrscheinlich, dass überhaupt eine perfekte Aufteilung existiert, und man muss alle Möglichkeiten durchprobieren, um die beste Aufteilung zu finden (harte Phase).

Zwischen der einfachen und der harten Phase beobachtet man einen Übergang, den man in Analogie zur statistischen Physik Phasenübergang nennt. An diesem Phasenübergang fällt die Wahrscheinlichkeit, eine perfekte Aufteilung zu finden, sprunghaft von 1 in der einfachen Phase auf 0 in der harten Phase. Mit wachsender Anzahl N der Zahlen wird der Übergang immer schärfer.

Die Lage des Phasenübergangs in Abhängigkeit von der Anzahl und der Größe der einzelnen Zahlen lässt sich mit Methoden der statistischen Physik berechnen.

Komplexität

Das Partitionsproblem gehört zu den 21 klassischen NP-vollständigen Problemen, von denen Richard Karp 1972 die Zugehörigkeit zur Klasse der NP-vollständigen Probleme zeigen konnte.

Es hat eine „worst-case-Laufzeit“, die exponentiell mit der Anzahl der Zahlen N wächst, das heißt im schlimmsten Fall benötigt ein Algorithmus zur Lösung des Entscheidungsproblem eine Rechenzeit, die exponentiell mit N ansteigt. In vielen Fällen liegt die tatsächlich benötigte Rechenzeit jedoch deutlich darunter: In der einfachen Phase stößt der Algorithmus schnell auf eine der vielen perfekten Lösungen und kann das Entscheidungsproblem somit mit „ja, es gibt eine perfekte Lösung“ beantworten und die Suche abbrechen. Auch in der harten Phase können geeignete Algorithmen (z.B. der cBLDM-Algorithmus^[1]) die Suche schnell mit einer negativen Entscheidung abschließen, falls keine Lösung existiert. Die „schwierigsten“ Probleme liegen somit direkt am Phasenübergang, wo erst alle 2^{N − 1} Aufteilungen durchprobiert werden müssen, bevor das Problem entschieden werden kann.

Quellen

1. ↑ S. Mertens: A complete anytime algorithm for balanced number partitioning, arXiv:cs/9903011