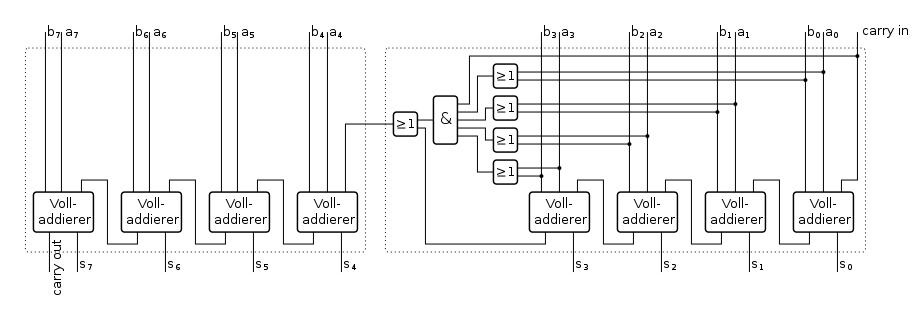
Paralleladdierer mit Übertragsumleitung

Ein Paralleladdierer mit Übertragsumleitung bzw. Carry-Skip-Addierer (englisch carry = Übertrag, to skip = überspringen) ist ein Addiernetz, dient also der Addition mehrstelliger Binärzahlen.

Er ist eine Erweiterung des Carry-Ripple-Addierers, enthält also einen Halb- und mehrere Volladdierer. Er bietet den Vorteil, dass die Worst-Case-Laufzeit verbessert wird, indem dem Problem der Übertragspropagation entgegengewirkt wird. Er ist zwar etwas langsamer als der Carry-Look-Ahead-Addierer, dafür aber günstiger, da weniger Gatter benötigt werden.

Hierzu werden die Volladdierer in Gruppen aufgeteilt. Eine schnelle Zusatzlogik ermittelt, ob sich ein Übertrag durch die gesamte Gruppe propagiert, was im Worst Case der Fall ist. Die Zusatzlogik untersucht dazu, ob in die Gruppe ein Übertrag eingeht und außerdem bei jedem der Eingangspaare (a_i, b_i) der Gruppe jeweils mindestens eine 1 anliegt.

In diesem Fall meldet die Zusatzlogik der nächsten Gruppe den Übertrag, so dass die Berechnung ihres Ergebnisses schon beginnen kann. Für die letzte Gruppe ist keine Zusatzlogik nötig.

Schaltbild eines 4-Bit Carry-Skip-Addierer kaskadiert mit einem normalen 4-Bit Addierer