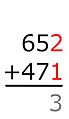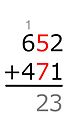Addition

+

Die Addition (lat. addere hinzufügen), umgangssprachlich auch Plus-Rechnen genannt, ist eine der vier Grundrechenarten in der Arithmetik. In der Grundschule und in der Umgangssprache verwendet man meist den Ausdruck Zusammenzählen für die Addition von zwei oder mehr Zahlen.

Das Zeichen für die Addition ist das Pluszeichen „+“. Es wurde 1489 von Johannes Widmann eingeführt.

Beispiel: 2 + 3 = 5 wird gelesen als „zwei plus drei (ist) gleich fünf“ oder umgangssprachlich „zwei und drei ergibt fünf“.

Die Elemente einer Addition werden Summanden und das Ergebnis Summe genannt.

Summe = erster Summand + zweiter Summand

oder

erster Summand + zweiter Summand = Summe

Aus dem Englischen kommend wird der erste Summand gelegentlich auch Augend genannt. Der zweite Summand heißt dann Addend.

Summe = Augend + Addend

Die Umkehroperation der Addition ist die Subtraktion. Sie wird als Addition mit der Gegenzahl aufgefasst.

Rechenregeln der Addition

Die Reihenfolge der Summanden ist egal, es ergibt sich trotzdem der gleiche Wert der Summe. Ob man 6 + 7 oder 7 + 6 addiert, man erhält jeweils 13 als Ergebnis (Kommutativgesetz oder Vertauschungsgesetz der Addition).

Bei der Addition dürfen Klammern umgesetzt oder weggelassen werden, es ergibt sich trotzdem der gleiche Wert der Summe (Assoziativgesetz oder Verbindungsgesetz der Addition).

Formell gelten bei der Addition folgende elementare Rechengesetze (x, y und z sind reelle Zahlen):

• Assoziativgesetz (Verbindungsgesetz) der Addition: (x + y) + z = x + (y + z) = x + y + z
• Kommutativgesetz (Vertauschungsgesetz) der Addition: x + y = y + x
• Das neutrale Element ist 0: x + 0 = x
• Das inverse Element zu x ist − x

Addition in verschiedenen Mengen

Die Addition kann ohne Ausnahme innerhalb der Mengen der natürlichen, der ganzen, der rationalen und der reellen Zahlen ausgeführt werden. Auch andere Mengen wie die der komplexen Zahlen besitzen eine Verknüpfung, die als Addition bezeichnet wird, weil sie denselben formalen Rechenregeln genügt.

Addition nennt man eine Reihe mathematischer Verknüpfungen, die alle die folgenden Eigenschaften haben:

• Sie sind assoziativ und kommutativ
• Sie erfüllen zusammen mit einer Multiplikation das Distributivgesetz

In den meisten Fällen ergibt die Addition zusammen mit ihrer Definitionsmenge eine abelsche Gruppe. Wichtigste Ausnahme ist die Addition auf den natürlichen Zahlen, wegen der wie oben erwähnt fehlenden Inversen (negativen Zahlen).

Ausgehend von den Peano-Axiomen lässt sich die Addition auf den natürlichen Zahlen folgendermaßen definieren:

• n + 0 = n
• n + m' = (n + m)'

n' bezeichnet den Nachfolger von n, der aufgrund der Peano-Axiome eindeutig bestimmt ist. Da 1 der Nachfolger von 0 ist, gilt

• n + 1 = n + 0' = (n + 0)' = n'.

Der Nachfolger von n stimmt also mit n + 1 überein.

Schriftliche Addition

Die schriftliche Addition ist eine der grundlegenden Kulturtechniken, die bereits in den ersten Schuljahren der Grundschule erlernt wird. Die Beherrschung der schriftlichen Addition ist auch Voraussetzung für das Erlernen der schriftlichen Multiplikation.

Traditionelles Verfahren

Bei dem Verfahren, dass u.a. im deutschsprachigen Raum an den Grundschulen gelehrt wird, werden die zu addierenden Zahlen so übereinander geschrieben, dass entsprechende Stellen untereinander stehen (Einer über Einern, Zehner über Zehnern, usw.). Die Ziffern werden dann – von rechts nach links – Stelle für Stelle aufaddiert; das Zwischenergebnis wird unten notiert, jedoch nur die letzte Stelle. Ist das Zwischenergebnis mehrstellig, so entstehen Überträge, die beim Abarbeiten der jeweils nächsten Spalte berücksichtigt werden müssen.

Beispiel:

• 

  2+1=3

• 

  5+7=12
  Die 1 wird als Übertrag der nächsten (links benachbarten) Ziffernspalte zugeschlagen.

• 

  1+6+4=11

Weitere Notationsmöglichkeit

Summen können auch mittels des Summensymbols Σ (nach dem großen griechischen Buchstaben Sigma) notiert werden:

$\sum_{i=m}^n x_i = x_m + x_{m+1} + x_{m+2} + ... + x_{n-1} + x_n$

Unter das Sigma wird die Zählvariable (in diesem Fall i) geschrieben. Ihr kann ein Startwert (hier: m) durch die Verbindung mit einem Gleichheitszeichen zugewiesen werden. Erfolgt diese Zuweisung nicht, so bedeutet das eine Summierung über alle möglichen i. Über dem Sigma steht der Endwert (hier: n). Zwischen dem Startwert und dem Endwert wird die Zählvariable jeweils um Eins erhöht. Um die Summe berechnen zu können, müssen n und m ganze Zahlen sein. Im Fall n = m besteht die Summe aus einem Summanden, im Fall n < m wird sie als 0 definiert.

Bildet man eine Summe aus unendlich vielen Ausdrücken, so wird diese unendliche Reihe genannt. Man schreibt dafür als Unter- bzw. Obergrenze das Symbol für minus bzw. plus Unendlich: $-\infty$ bzw. $\infty$.

Der Umgang mit diesem Symbol sowie einige häufig vorkommende Summen werden im Artikel Summe beschrieben.

Siehe auch

• Addition (Begriffsklärung)
• Addition von Vektoren
• Arithmetik in Stellenwertsystemen
• Addierstift
• Pythagoreische Addition

Weblinks

 Wiktionary: Addition – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Äpfel - Freeware-Übungsprogramm zur schriftlichen Addition
• Exerceamus – Schriftliche Addition Online-Lernprogramm und Trainer
• Schriftliche Addition online (für selbst gewählte Zahlen)