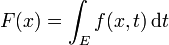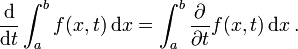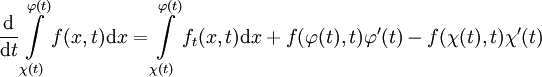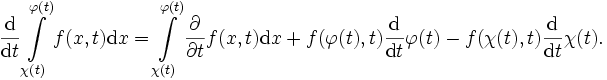Parameterintegral — Als Parameterintegral wird in der Analysis ein Integral mit einem Parameter bezeichnet. Ein wichtiges Beispiel ist die Gammafunktion. Inhaltsverzeichnis 1 Definition des Parameterintegrals 2 Stetigkeit von Parameterintegralen 3 … Deutsch Wikipedia
Euler-Konstante — γ Die Euler Mascheroni Konstante (nach den Mathematikern Leonhard Euler und Lorenzo Mascheroni), auch Eulersche Konstante, ist eine wichtige mathematische Konstante, die mit dem griechischen Buchstaben γ (gamma) bezeichnet wird. Ihre Definition… … Deutsch Wikipedia
Euler-Mascheroni-Konstante — γ Die Euler Mascheroni Konstante (nach den Mathematikern Leonhard Euler und Lorenzo Mascheroni), auch Eulersche Konstante, ist eine wichtige mathematische Konstante, die mit dem griechischen Buchstaben γ (Gamma) bezeichnet wird … Deutsch Wikipedia
Eulerkonstante — γ Die Euler Mascheroni Konstante (nach den Mathematikern Leonhard Euler und Lorenzo Mascheroni), auch Eulersche Konstante, ist eine wichtige mathematische Konstante, die mit dem griechischen Buchstaben γ (gamma) bezeichnet wird. Ihre Definition… … Deutsch Wikipedia
Eulersche Konstante — γ Die Euler Mascheroni Konstante (nach den Mathematikern Leonhard Euler und Lorenzo Mascheroni), auch Eulersche Konstante, ist eine wichtige mathematische Konstante, die mit dem griechischen Buchstaben γ (gamma) bezeichnet wird. Ihre Definition… … Deutsch Wikipedia
Gamma (Euler-Konstante) — γ Die Euler Mascheroni Konstante (nach den Mathematikern Leonhard Euler und Lorenzo Mascheroni), auch Eulersche Konstante, ist eine wichtige mathematische Konstante, die mit dem griechischen Buchstaben γ (gamma) bezeichnet wird. Ihre Definition… … Deutsch Wikipedia
Leibniz-Regel — Unter der Leibnizregel versteht man zwei verschiedene Begriffe: Sie dient als eine andere Bezeichnung für die Produktregel der Differentiation Sie bezeichnet die Leibnizregel für Parameterintegrale … Deutsch Wikipedia
Leibnizregel — Als Leibnizregel bezeichnet man: in der Analysis die Produktregel der Differenziation in der Algebra, die definierende Eigenschaft einer Derivation in der Analysis die Leibnizregel für Parameterintegrale Diese Seite ist eine … Deutsch Wikipedia
Verallgemeinerte Kettenregel — Die verallgemeinerte Kettenregel ist in der mehrdimensionalen Analysis eine Verallgemeinerung der Kettenregel von Funktionen einer Variablen auf Funktionen und Abbildungen mehrerer Variablen. Sie besagt, dass die Verkettung von (total)… … Deutsch Wikipedia
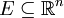 messbar und nicht die leere Menge. Ferner sei
messbar und nicht die leere Menge. Ferner sei 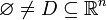 und
und 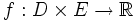 . Für f(x,t) ist
. Für f(x,t) ist 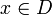 und
und 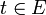 . f sei bezüglich t integrierbar über E. Dann heißt
. f sei bezüglich t integrierbar über E. Dann heißt 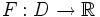
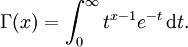
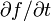 stetig, kann man "unter dem Integral differenzieren":
stetig, kann man "unter dem Integral differenzieren": und f gilt
und f gilt