- Parameterschätzung
-
Das Konfidenzintervall (auch Vertrauensbereich oder Mutungsintervall genannt) ist ein Begriff aus der mathematischen Statistik. Er sagt etwas über die Präzision der Lageschätzung eines Parameters (zum Beispiel eines Mittelwertes) aus. Das Vertrauensintervall schließt einen Bereich um den geschätzten Wert des Parameters ein, der – vereinfacht gesprochen – mit einer zuvor festgelegten Wahrscheinlichkeit die wahre Lage des Parameters trifft. Ein Vorteil des Konfidenzintervalls gegenüber der Punktschätzung eines Parameters ist, dass man an ihm direkt die Signifikanz ablesen kann. Ein zu breites Vertrauensintervall weist auf einen zu geringen Stichprobenumfang hin. Entweder ist die Stichprobe tatsächlich "klein", oder das untersuchte Phänomen ist so variabel, dass nur durch eine unrealistisch große Stichprobe ein Konfidenzintervall von akzeptabler Breite erreicht werden könnte.
Inhaltsverzeichnis
Beispiel einer Anwendung
Ein Physikdoktorand misst die ausstrahlende Wellenlänge bei einem Experiment unter zwei verschiedenen Bedingungen. Leider ist das Messgerät 10 Jahre alt und die Mechanik der Optik etwas wackelig. Obwohl also aufgrund des Versuchsansatzes nur das Licht einer Wellenlänge pro Bedingung erwartet wird, streut das Ergebnis bei unabhängigen Messungen. Der Physikdoktorand geht davon aus, dass das Messgerät mit gleicher Wahrscheinlichkeit zu große wie zu kleine Wellenlängen misst und dass extreme Messfehler unwahrscheinlicher sind als Messwerte nahe dem wahren Wert (Normalverteilung).
Daraufhin rechnet er aus den Ergebnissen der Einzelmessungen den arithmetischen Mittelwert aus. Für jede Bedingung einen Mittelwert. Er zeigt die Daten seinem Doktorvater, der wissen will, wie stark die Streuung der Messwerte war.
Jetzt rechnet der Doktorand den Standardfehler aus, um ein Maß für die Genauigkeit seiner beiden Mittelwerte zu bekommen und diese graphisch (als Fehlerbalken um den Mittelwert) darstellen zu können. Der Standardfehler bezieht neben der Streuung die Anzahl der Einzelmessungen mit ein. Je mehr Einzelmessungen vorgenommen werden desto näher kommt der errechnete Mittelwert dem wahren Wert und desto kleiner ist auch der Standardfehler.
Der Doktorvater ist aber immer noch nicht zufrieden, denn jetzt will er wissen, ob sich die zwei errechneten Mittelwerte unter den zwei unterschiedlichen Bedingungen statistisch signifikant voneinander unterscheiden oder ob es nur aufgrund der Ungenauigkeit des Gerätes zu unterschiedlichen Mittelwerten kommt. Daraufhin rechnet der Doktorand die Vertrauensintervalle um die Mittelwerte aus, die in Abhängigkeit von der Streuung und der Anzahl der Einzelmessungen den Bereich angeben, der jeweils den wahren Wert mit hoher Wahrscheinlichkeit mit einschließt. Wählt man ein 95 %-Konfidenzintervall (das heißt: in 95 von 100 Fällen enthalten die errechneten Intervallgrenzen den wahren Wert) und die Balken des Konfidenzintervalls der beiden Mittelwerte überschneiden sich nicht, dann werden die Mittelwerte in der Regel als signifikant unterschiedlich bezeichnet (wird häufig mit einem * markiert); hierbei handelt es sich aber nur um eine Faustregel: es gibt sehr wohl Fälle, wo sich die Unter- und Obergrenze zweier KI nicht überschneiden und die Mittelwerte nicht signifikant unterschiedlich sind. Bei einem 99 %-Konfidenzintervall und fehlender Überlappung gelten sie als hochsignifikant unterschiedlich (Markierung: **).
Beschreibung des Verfahrens
Man interessiert sich für den unbekannten Verteilungsparameter einer Zufallsvariablen einer Grundgesamtheit. Der „wahre“ Parameter γ (Gamma) für eine Grundgesamtheit wird durch eine Schätzfunktion g aus einer Stichprobe vom Umfang n geschätzt. Es wird davon ausgegangen, dass die Stichprobe in etwa die Grundgesamtheit widerspiegelt und dass deshalb die Schätzung in der Nähe des wahren Parameters liegen müsste. Die Schätzfunktion ist eine Zufallsvariable mit einer Verteilung, die den Parameter γ enthält.
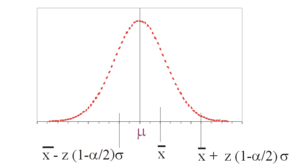
Man kann zunächst mit Hilfe der Verteilung ein Intervall angeben, das den unbekannten wahren Parameter γ mit einer Wahrscheinlichkeit 1−α einschließt. 1−α wird Konfidenzkoeffizient genannt. Ermitteln wir z. B. das 95 %-Konfidenzintervall für den wahren Erwartungswert μ einer Population, dann bedeutet dies, dass wir bei durchschnittlich 5 von 100 gleichgroßen Zufallsstichproben ein Konfidenzintervall ermitteln, das den Erwartungswert nicht enthält.
Das Verfahren wird anhand eines normalverteilten Merkmals mit dem unbekannten Erwartungswert μ und der bekannten Varianz σ2 demonstriert: Es soll der Erwartungswert μ dieser Normalverteilung geschätzt werden. Verwendet wird die erwartungstreue Schätzfunktion: der Stichprobenmittelwert
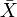 .
.Der Erwartungswert der Population wird anhand unserer Stichprobe geschätzt
wobei die Zufallsvariable Xi (i=1,…,n) für die i-te Beobachtung (vor der Ziehung der Stichprobe) steht. Es ist
Die Grenzen des Intervalls
in dem
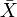 mit der Wahrscheinlichkeit 1−α liegt, bestimmen sich aus der Beziehung
mit der Wahrscheinlichkeit 1−α liegt, bestimmen sich aus der Beziehung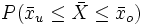 .
.
Man standardisiert und erhält für die standardisierte Zufallsvariable
die Wahrscheinlichkeit
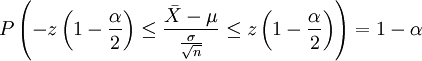 ,
,
wobei z(1-α/2) das (1-α/2)-Quantil der Standardnormalverteilung ist. Löst man nach μ auf, resultiert aus dem Zufallsintervall
das (1−α)-Konfidenzintervall für μ
Das durch
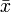 bestimmte Intervall überdeckt den wahren Parameter μ also mit einer Wahrscheinlichkeit von 1−α. Ist die Stichprobe aber extrem ausgefallen, überdeckt das Intervall den Parameter nicht. Dies ist in α·100 % aller Stichproben der Fall.
bestimmte Intervall überdeckt den wahren Parameter μ also mit einer Wahrscheinlichkeit von 1−α. Ist die Stichprobe aber extrem ausgefallen, überdeckt das Intervall den Parameter nicht. Dies ist in α·100 % aller Stichproben der Fall.Von besonderem Interesse ist die Breite des Konfidenzintervalls. Diese bestimmt sich durch die Standardabweichung der Schätzfunktion. Durch Erhöhung des Stichprobenumfangs kann die Breite verringert werden. Erwünscht ist in der Regel ein möglichst schmales Konfidenzintervall, denn dies weist auf eine genaue Schätzung hin.
Ausgewählte Konfidenzintervalle
Übersicht
Erwartungswert eines normalverteilten Merkmals mit bekannter Varianz: ![\left[ { \bar x-z(1-\begin{matrix} \frac {\alpha}{2} \end{matrix}) \frac {\sigma}{\sqrt{n}} \ ; \ \bar x+z(1-\begin{matrix} \frac {\alpha}{2} \end{matrix}) \frac {\sigma}{\sqrt{n}}} \right]](/pictures/dewiki/50/2122c505414eece3b1a324013c496779.png)
Erwartungswert eines normalverteilten Merkmals mit unbekannter Varianz. Die Varianz der Grundgesamtheit wird durch die korrigierte Stichprobenvarianz geschätzt.
t(1-α;n-1) ist das 1−α-Quantil der t-Verteilung mit n-1 Freiheitsgraden.
Für n > 30 kann das Quantil der t-Verteilung näherungsweise durch das entsprechende Quantil der Standardnormalverteilung ersetzt werden.
![\left[ { \bar x-t(1-\begin{matrix} \frac {\alpha}{2} \end{matrix}, n-1) \frac {s}{\sqrt{n}} \ ; \ \bar x+t(1-\begin{matrix} \frac {\alpha}{2} \end{matrix}, n-1) \frac {s}{\sqrt{n}}} \right]](/pictures/dewiki/100/d216ab466cfa3fa87076ed2ed28d4368.png)
Erwartungswert eines unbekannt verteilten Merkmals mit unbekannter Varianz, falls n > 50 ist. ![\left[ { \bar x-z(1-\begin{matrix} \frac {\alpha}{2} \end{matrix}) \frac {s}{\sqrt{n}} \ ; \ \bar x+z(1-\begin{matrix} \frac {\alpha}{2} \end{matrix}) \frac {s}{\sqrt{n}}} \right]](/pictures/dewiki/52/46e65113badf09a3d05781783751531c.png)
Varianz eines normalverteilten Merkmals. χ2(p;k) ist das p-Quantil der χ2-Verteilung mit k Freiheitsgraden.
![\left[ \frac {(n-1)s^2}{\chi^2 (1- \frac {\alpha}{2}, n-1)} \ ; \ \frac {(n-1)s^2}{ \chi^2(\frac {\alpha}{2}; n-1)} \right]](/pictures/dewiki/56/801cf36bb3ae9cae528546fc9660190d.png)
Anteilswert θ einer dichotomen Grundgesamtheit bei einem Urnenmodell mit Zurücklegen, falls ist, mit
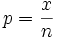 und x als Realisation der binomialverteilen Zufallsvariablen.
und x als Realisation der binomialverteilen Zufallsvariablen.![\left[ { p-z \left( 1-\frac {\alpha}{2} \right) \sqrt {\frac {p(1-p)}{n}} \ ; \ p+z \left( 1-\frac {\alpha}{2} \right) \sqrt {\frac {p(1-p)}{n}}} \right]](/pictures/dewiki/57/992c01d6ba487fc9d6d3910fb691d921.png)
Anmerkungen
Ist die Zahl N der Elemente in der Grundgesamtheit bekannt, kann für den Parameter auch ein Konfidenzintervall für ein Urnenmodell ohne Zurücklegen angegeben werden. Hier wird die Standardabweichung noch mit einem Korrekturfaktor modifiziert.
Wenn bei einem binomialverteilten Merkmal der Stichprobenumfang
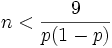 ist, kann ein exaktes Konfidenzintervall für den Anteilswert mit Hilfe der F-Verteilung angegeben werden.
ist, kann ein exaktes Konfidenzintervall für den Anteilswert mit Hilfe der F-Verteilung angegeben werden.Anwendung bei Hypothesentests
Konfidenzintervalle kommen auch bei Hypothesentests zum Einsatz: Testet man von einem Parameter θ die Nullhypothese: θ = θ0, dann ist das Kriterium für das Ablehnen der Nullhypothese bei Signifikanzniveau α, ob das entsprechende (1-α)-Konfidenzintervall den Wert θ0 enthält oder nicht.
Bemerkung
Konfidenzintervalle können gelegentlich auch Hypothesentests ersetzen. Beispielsweise testet man in der Regressionsanalyse, ob im multiplen Regressionsmodell mit der geschätzten Regressionshyperebene
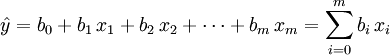 mit x0 = 1
mit x0 = 1
die wahren Regressionskoeffizienten βj (j = 1, … , m) gleich Null sind. Wenn die Hypothese nicht abgelehnt wird, sind die entsprechenden Regressoren xj vermutlich für die Erklärung der abhängigen Variablen y unerheblich. Eine entsprechende Information liefert das Konfidenzintervall für einen Regressionskoeffizienten: Überstreicht das Konfidenzintervall die Null, kann mit einer Wahrscheinlichkeit von 1-α der Regressionskoeffizient ebenso gut Null sein, d. h. er ist statistisch insignifikant.
Beispiel für ein Konfidenzintervall
Ein Unternehmen möchte flächendeckend auf dem Markt ein neues Spülmittel einführen. Um die Käuferakzeptanz auszuloten, wird in einem Supermarkt dieses Produkt mit hohem Werbeaufwand platziert. Es soll mit dieser Aktion der durchschnittliche tägliche Absatz in einem Supermarkt dieser Größe geschätzt werden. Man definiert nun den täglichen Absatz als Zufallsvariable X [Stück] mit den unbekannten Parametern Erwartungswert μ und der Varianz σ2. Man geht auf Grund langjähriger Beobachtungen hier davon aus, dass X annähernd normalverteilt ist. Die Marktforschungsabteilung hat einen Konfidenzkoeffizienten von 0,95 als ausreichend erachtet. Es wird nun 16 Tage lang der tägliche Absatz erfasst. Es hat sich beispielsweise ergeben
Absatz x 110 112 106 90 96 118 108 114 107 90 85 84 113 105 90 104 Bei normalverteilter Grundgesamtheit mit unbekannter Varianz wird das Konfidenzintervall für den Erwartungswert angegeben als
Es ist
und
Es ist das (1-α/2)-Quantil der t-Verteilung mit 15 Freiheitsgraden
Das 95 %-Konfidenzintervall berechnet sich dann als
In 95 % aller Fälle beinhaltet also das Intervall des durchschnittlichen täglichen Absatzes an Spülmittelflaschen zwischen ca. 96 und 108 Stück den wahren Mittelwert. Dieses Intervall ist relativ schmal, so dass man gut mit dieser Information planen kann.
Konfidenzintervall für eine Wahrscheinlichkeit
Eine weitere Möglichkeit, den Vertrauensbereich (Konfidenzintervall) für eine Wahrscheinlichkeit (Anteilswert einer dichotomen Grundgesamtheit) exakt zu bestimmen, ist die Verwendung der Betaverteilung. Mehr Informationen finden sich im Artikel Konfidenzintervall einer unbekannten Wahrscheinlichkeit.
Weblinks
Wikimedia Foundation.


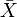
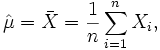
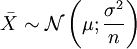
![[\bar x_u; \bar x_o] ,](/pictures/dewiki/99/c24465b1b12eb5b9aec13d2aff0e3156.png)
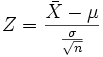
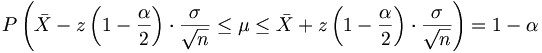
![\left[ { \bar x-z \left( 1-\frac {\alpha}{2} \right) \cdot \frac {\sigma}{\sqrt{n}} \ ; \ \bar x+z \left( 1-\frac {\alpha}{2} \right) \cdot \frac {\sigma}{\sqrt{n}}} \right].](/pictures/dewiki/51/33c6626282147366b360ab9fa5eb0828.png)
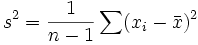
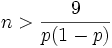
![\left[ { \bar x-t \left( 1-\frac {\alpha}{2}; n-1 \right) \frac {s}{\sqrt{n}} \ ; \ \bar x+t \left( 1-\frac {\alpha}{2} ; n-1 \right) \frac {s}{\sqrt{n}}} \right]](/pictures/dewiki/101/e2764f7c34af56cf837f556ca0db6cf4.png)
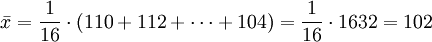
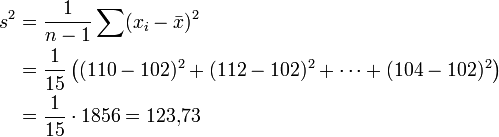
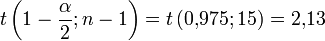
![\left[ { 102 - 2{,}13 \frac {\sqrt{123{,}73}} {\sqrt{16}} ; 102 + 2{,}13 \frac {\sqrt{123{,}73}} {\sqrt{16}} } \right] = [102 -5{,}92; 102 + 5{,}92] = [96{,}08; 107{,}92]](/pictures/dewiki/101/e2d82a53828cca5b0307f29512e380ef.png)