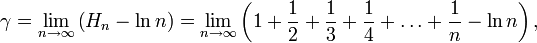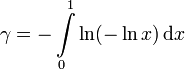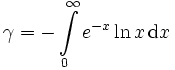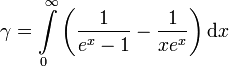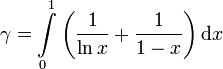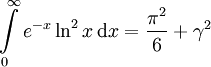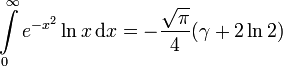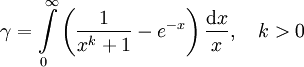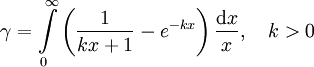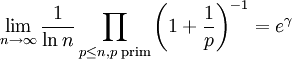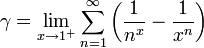Eulersche Konstante

γ

Die Euler-Mascheroni-Konstante (nach den Mathematikern Leonhard Euler und Lorenzo Mascheroni), auch Eulersche Konstante, ist eine wichtige mathematische Konstante, die mit dem griechischen Buchstaben γ (gamma) bezeichnet wird.

Ihre Definition lautet:

$\gamma = \lim_{n\to\infty} \left(H_n - \ln n\right) = \lim_{n\to\infty} \left(1 + \frac12 + \frac13 + \frac14 + \ldots + \frac1{n} - \ln n\right),$

wobei H_n die Harmonische Reihe bezeichnet.

Ihr numerischer Wert ist auf 100 dezimale Nachkommastellen genau (Folge A001620 in OEIS):

γ = 0,5772156649015328606065120900824024310421593359399235988057672348848677267776646709369470632917467495.

Derzeit (13. Jan. 2009) sind 14.900.000.000 dezimale Nachkommastellen bekannt.^[1]

Trotz großer Anstrengungen ist bis heute unbekannt, ob diese Zahl rational oder irrational, ob sie algebraisch oder transzendent ist. Es wird aber stark vermutet, dass sie zumindest eine irrationale Zahl ist. Den ersten konkreten Beweisversuch hierzu hat 1926 Paul Émile Appell mit Hilfe der unten genannten Entwicklung von Joseph Ser unternommen.

Im Gegensatz zur Kreiszahl π, die jeweils bei Umfang und Fläche eines Kreises mit rationalem Radius auftritt, ist für die Eulersche Konstante außerhalb der Mathematik kein Beispiel eines direkten Vorkommens bekannt. Es gibt zwar viele praktische Probleme, die auf die Summierung der endlichen harmonischen Reihe H_n führen wie etwa das Problem der optimalen Sitzreihen-Erhöhung in Theatern und Kinos. Dort handelt es sich aber immer um endlich viele Terme, so dass kein Grenzübergang 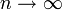$n\to\infty$ zustande kommt, der für das Auftreten von γ erforderlich wäre. Beim Kreis, der aus unendlich vielen Punkten gebildet wird, ist ein solcher Grenzprozess bereits enthalten.

Die Euler-Mascheroni-Konstante in mathematischen Problemen

Die eulersche Konstante tritt in der Mathematik sehr häufig und manchmal auch ganz unerwartet in unterschiedlichen Teilgebieten auf. Hauptsächlich tritt sie bei Grenzwertprozessen der Differential- und Integralrechnung auf. Das Auftreten lässt sich (wie auch bei anderen mathematischen Konstanten) so unterteilen:

1. Als Funktionswert oder Grenzwert von Speziellen Funktionen.

Der Wert γ ist die negative Ableitung der Gammafunktion an der Stelle 1, also

$\Gamma^\prime(1)=-\gamma$.

$\lim_{s\to 1}\left(\zeta(s)-\frac{1}{s-1}\right)=\gamma$.

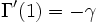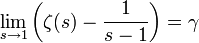Hierbei bezeichnet ζ(s) die riemannsche Zeta-Funktion.

2. In Entwicklungen spezieller Funktionen, z.B. bei der Reihenentwicklung des Integrallogarithmus von Leopold Schendel, der Besselfunktionen oder der Weierstraß'schen Darstellung der Gammafunktion.

3. Integraldarstellungen

Hier gibt es eine reichhaltige Fülle, z.B.:

$\gamma = -\int\limits_0^1 \ln(-\ln x)\, \mathrm{d}x$

$\gamma = -\int\limits_0^\infty e^{-x}\ln x\, \mathrm{d}x$

$\gamma = \int\limits_0^\infty\left(\frac1{e^x-1} - \frac1{xe^x}\right) \mathrm dx$

$\gamma = \int\limits_0^1\left(\frac 1{\ln x} + \frac 1{1-x}\right) \mathrm dx$

oder auch

$\int\limits_0^\infty e^{-x} \ln^2 x\,\mathrm dx = \frac{\pi^2}6 +\gamma^2$

$\int\limits_0^\infty e^{-x^2} \ln x\,\mathrm dx = -\frac{\sqrt\pi}4 (\gamma +2\ln 2)$

Es gibt auch sehr viele invariante Parameterintegrale, z.B.:

$\gamma = \int\limits_0^\infty \left(\frac1{x^k+1} - e^{-x}\right)\frac{\mathrm{d}x}{x},\quad k>0$

$\gamma = \int\limits_0^\infty \left(\frac1{kx+1} - e^{-kx}\right)\frac{\mathrm{d}x}{x},\quad k>0$

Ferner gibt es eine ebenso reichhaltige Fülle an unendlichen Summen und Produkten, etwa

$\lim_{n\to\infty} \frac 1{\ln n} \prod_{p\le n, p\text{ prim}} \left( 1+\frac 1p \right)^{-1} = e^\gamma$

$\lim_{n\to\infty} \frac 1{\ln n} \prod_{p\le n, p\text{ prim}} \left( 1+\frac 1p \right) = \frac{6e^\gamma}{\pi^2}$

$\gamma = \lim_{x\to 1^{+}} \sum_{n=1}^\infty \left(\frac 1{n^x} -\frac 1{x^n} \right)$

4. Reihendarstellungen sind im Gegensatz zu π prinzipiell seltener. Als Beispiele von Reihen mit rationalen Gliedern sind nur die Reihen von Euler, Giovanni Enrico Eugenio Vacca, Ramanujan und Joseph Ser bekannt. An Reihen mit irrationalen Gliedern gibt es unzählige Variationen, deren Glieder aus rational gewichteten Werten der riemannschen Zeta-Funktion an den ungeraden Argumentstellen ζ(3), ζ(5), ... bestehen. Ein Beispiel einer besonders schnell konvergenten Reihe ist:

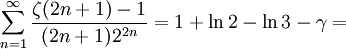$\sum_{n=1}^{\infty}\frac{\zeta(2n+1)-1}{(2n+1)2^{2n}} = 1 + \ln2 - \ln3 - \gamma =$ 0,0173192...

Bezeichnungen

Man kann sagen, dass die Eulersche Konstante diejenige Konstante mit den meisten Bezeichnungen ist. Euler selbst bezeichnete sie mit C und gelegentlich mit O bzw. n. Es ist jedoch zweifelhaft, ob er damit ein eigenständiges Symbol für seine Konstante einführen wollte. Mascheroni bezeichnete die Konstante nicht - wie oft behauptet - mit γ, sondern ausschließlich mit A. Andere Mathematiker verwenden die Bezeichnungen 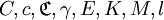$C, c, \mathfrak{C}, \gamma, E, K, M, l$. Der Ursprung der heute üblichen Bezeichnung γ ist ein offenes Problem. Als gesichert gilt, dass Carl Anton Bretschneider (1808−1878) in seiner Arbeit 1837 Theoriae logarithmi integralis lineamenta nova die Bezeichnung γ verwendet. Das γ-Missverständnis rührt von dem viel zitierten, aber nie überprüften Artikel von James Whitbread Lee Glaisher her:

„Euler's constant which throughout this note will be called γ after Mascheroni, De Morgan, &c. [...]
It is clearly convenient that the constant should generally be denoted by the same letter. Euler used C and O for it; Legendre, Lindman, &c., C; De Haan A; and Mascheroni, De Morgan, Boole, &c., have written it γ, which is clearly the most suitable, if it is to have a distinctive letter assigned to it. It has sometimes (as in Crelle, t.57, p.128) been quoted as Mascheroni's constant, but it is evident that Euler's labours have abundantly justified his claim to its being named after him.“

– Glaisher: On the history of Euler's constant, 1872, p.25,30

Einzelnachweise

1. ↑ http://www.numberworld.org/nagisa_runs/computations.html

Literatur

• Lorenzo Mascheroni. Adnotationes ad calculum integralem Euleri, in quibus nonnulla problemata ab Eulero proposita resolvuntur. Ticini: Galeati, 1790. (Reprint: Leonhardi Euleri Opera Omnia, Ser.1, Vol.12. Teubner, Leipzig 1915, S.415−542
• Carl Anton Bretschneider. Theoriae logarithmi integralis lineamenta nova. Crelle Journal, Bd.17 (1837), S.257−285
• James Whitbread Lee Glaisher. On the history of Euler's constant. Messenger of mathematics, Bd.1 (1872), S.25−30
• Julian Havil: Gamma: Eulers Konstante, Primzahlstrände und die Riemannsche Vermutung. Springer, Berlin 2007, ISBN 978-3-540-48495-0

Weblinks

• Eric W. Weisstein: Euler-Mascheroni-Konstante auf MathWorld (englisch)
• Folge A002852 in OEIS (Kettenbruchentwicklung von γ)
• Folge A053977 in OEIS (Engel-Entwicklung von γ)