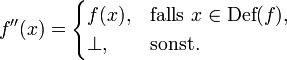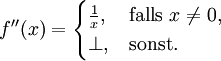- Partielle Abbildung
-
Eine partielle Funktion von der Menge X in die Menge Y ist eine rechtseindeutige Relation, das heißt eine Relation, in der jedes Element der Menge X höchstens einem Element der Menge Y zugeordnet wird. Der Begriff der partiellen Funktion ist in der Theoretischen Informatik, insbesondere in der Berechenbarkeitstheorie verbreitet.
Der Begriff der partiellen Funktion ist eine Verallgemeinerung des Begriffs der Funktion. Unter einer Funktion von X nach Y versteht man eine linkstotale, rechtseindeutige Relation, also eine Relation, in der jedem Element von X genau ein Element von Y zugeordnet ist. Jede Funktion von X nach Y ist also insbesondere eine partielle Funktion von X nach Y, aber nicht umgekehrt. Insofern ist der Begriff der partiellen Funktion irreführend. Um auszudrücken, dass eine partielle Funktion eine Funktion ist, sagt man gelegentlich, es handle sich um eine totale Funktion.
Als Definitionsbereich Def(f) der partiellen Funktion f bezeichnet man die Menge aller derjenigen Elemente aus X, denen ein Element aus Y zugeordnet ist. Eine partielle Funktion f ist also genau dann eine Funktion, wenn Def(f) = X gilt.
Eine partielle Funktion f von X in Y lässt sich auf zweierlei Arten als Funktion modellieren:
- als Funktion
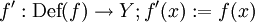 , oder
, oder - als Funktion
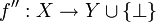 mit
mit
Der Wert
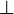 („bottom“ oder „undefiniert“) darf dazu nicht in Y sein.
(„bottom“ oder „undefiniert“) darf dazu nicht in Y sein.Schreibweisen
Für „f ist eine partielle Funktion von X nach Y“ schreibt man:
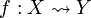 oder
oder 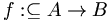 oder auch
oder auch 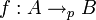 . Nicht empfehlenswert ist die Schreibweise
. Nicht empfehlenswert ist die Schreibweise 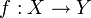 , denn sie definiert f als Funktion, was im Allgemeinen nicht wohldefiniert ist.
, denn sie definiert f als Funktion, was im Allgemeinen nicht wohldefiniert ist.Die Schreibweise „f(x) ist undefiniert“ oder sogar „f(x) = undefiniert“ ist problematisch, denn der Ausdruck f(x) ist ja dann gerade nicht zulässig. Klarer ist es zu sagen „f ist undefiniert an der Stelle x“ oder als Formel „
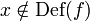 “.
“.Beispiele
- Die partielle Funktion
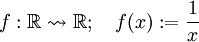 ist an der Stelle x = 0 undefiniert, weil die Division durch 0 in den reellen Zahlen unzulässig ist. Man kann bilden
ist an der Stelle x = 0 undefiniert, weil die Division durch 0 in den reellen Zahlen unzulässig ist. Man kann bilden 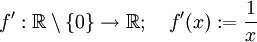
- oder
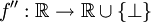 mit
mit
- partiell rekursive Funktionen
- ein unbeschränkter linearer Operator
Anwendungen
Wenn ein Algorithmus Eingaben aus der Menge X annimmt und Ausgaben aus der Menge Y liefert, dann berechnet er eine partielle Funktion von X nach Y. Der Definitionsbereich dieser Funktion ist die Menge aller Elemente aus X, für die der Algorithmus einen Wert liefert. Um einen Wert zu liefern, muss er insbesondere mit seiner Berechnung an ein Ende kommen (terminieren).
- als Funktion
Wikimedia Foundation.