Standardabweichung

Die Standardabweichung ist ein um 1860 von Francis Galton eingeführter Begriff der Statistik und der Wahrscheinlichkeitsrechnung und ein Maß für die Streuung der Werte einer Zufallsvariablen um ihren Mittelwert. Sie ist für eine Zufallsvariable X definiert als die positive Quadratwurzel aus deren Varianz und wird als $\sigma_X = \sqrt{\operatorname{Var}(X)}$ notiert.

Liegt eine Beobachtungsreihe $(x_1, x_2, \dots, x_N)$ der Länge N vor, so sind empirischer Mittelwert und empirische Standardabweichung die zwei wichtigsten Maßzahlen in der Statistik zur Beschreibung der Eigenschaften der Beobachtungsreihe.

Die Standardabweichung besitzt die gleiche Einheit wie die Messwerte der Beobachtungsreihe. Die Varianz dagegen wird mit der Einheit zum Quadrat notiert.

Als Abkürzung findet man neben σ in Anwendungen insbesondere für die empirische Standardabweichung oft s oder SD (für standard deviation), sowie m.F. für mittlerer Fehler. In der angewandten Statistik findet man häufig die Kurzschreibweise der Art „Ø 21 ± 4“, was als „Mittelwert 21 mit einer Standardabweichung von 4“ zu lesen ist.

Definition

Die Standardabweichung einer Zufallsvariablen X ist gleich der Quadratwurzel der Varianz $\operatorname{Var}(X)$. Sie ergibt sich also zu

$\sigma_X := \sqrt{\operatorname{Var}(X)} = \sqrt{\operatorname E\left((X-\operatorname E\left(X\right))^2\right)} \;\text{,}$

wobei $E(\cdot)$ den Erwartungswert bildet.

Beispiele und Faustformeln

Normalverteilung

Hintergrund der Berechnung

Intervalle um μ bei der Normalverteilung

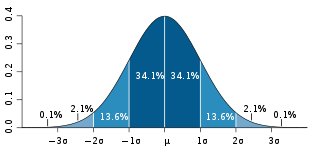
Normalverteilte Zufallsgrößen werden durch Angabe von Mittelwert μ und Standardabweichung σ vollständig beschrieben. Aus der Tabelle der Standardnormalverteilung ist ersichtlich, dass für normalverteilte Zufallsgrößen

68,3 % der Realisierungen im Intervall $\mu\pm\sigma$,

95,4 % im Intervall $\mu\pm 2\sigma$ und

99,7 % im Intervall $\mu\pm 3\sigma$

liegen. Da in der Praxis viele Zufallsgrößen annähernd normalverteilt sind, werden diese Werte aus der Normalverteilung oft als Faustformel benutzt. So lässt sich beispielsweise σ als die halbe Breite des Intervalls schätzen, welches die mittleren vier Sechstel der Werte in einer Stichprobe umfasst, siehe Quantil.

Werte außerhalb der zwei- bis dreifachen Standardabweichung werden oft als Ausreißer behandelt. Ausreißer können ein Hinweis auf grobe Fehler der Datenerfassung sein. Es kann den Daten aber auch eine stark schiefe Verteilung zu Grunde liegen. Andererseits liegt bei einer Normalverteilung im Durchschnitt ca. jeder 20. Messwert außerhalb der zweifachen Standardabweichung und ca. jeder 500. Messwert außerhalb der dreifachen Standardabweichung.

Ein Beispiel (mit Schwankungsbreite)

Die Körpergröße des Menschen ist näherungsweise normalverteilt. Bei einer Stichprobe von 1.284 Mädchen und 1.063 Jungen zwischen 14 und 18 Jahren wurde bei den Mädchen eine durchschnittliche Körpergröße von 166,3 cm (Standardabweichung 6,39 cm) und bei den Jungen eine durchschnittliche Körpergröße von 176,8 cm (Standardabweichung 7,46 cm) gemessen.^[1]

Demnach lässt obige Schwankungsbreite erwarten, dass 68 % der Mädchen eine Körpergröße im Bereich 166,3 cm ± 6,39 cm und 95 % im Bereich 166,3 cm ± 12,78 cm haben,

• 16 % [≈ (100 % - 68,3 %)/2] der Mädchen kleiner als 160 cm (und 16 % entsprechend größer als 173 cm) sind und
• 2,5 % [≈ (100 % - 95,4 %)/2] der Mädchen kleiner als 154 cm (und 2,5 % entsprechend größer als 179 cm) sind.

Für die Jungen lässt sich erwarten, dass 68 % eine Körpergröße im Bereich 176,8 cm ± 7,46 cm und 95 % im Bereich 176,8 cm ± 14,92 cm haben,

• 16 % der Jungen kleiner als 169 cm (und 16 % größer als 184 cm) und
• 2,5 % der Jungen kleiner als 162 cm (und 2,5 % größer als 192 cm) sind.

Diskrete Gleichverteilung, Würfel

Die diskrete Gleichverteilung auf den Zahlen $1,\dots,n$ hat einen Mittelwert von $\tfrac{n+1}{2}$ und eine Standardabweichung von $\sqrt{\tfrac{n^2-1}{12}}$. Das Ergebnis des Wurfes eines fairen Würfels hat also den Mittelwert 3,5 und eine Standardabweichung von etwa 1,7.

Diese Verteilung unterscheidet sich wesentlich von einer Normalverteilung, obige Faustformeln liefern daher keine zuverlässige Abschätzung. Die Faustformeln lassen erwarten, dass 68 % der Würfelergebnisse im Intervall 3,5±1,7, also zwischen 1,8 und 5,2 liegen und dabei etwa 16 % der Ergebnisse kleiner als 1,8 und ebenso viele größer als 5,2 sind. Die tatsächliche Wahrscheinlichkeit dafür, eine 1 oder 6 zu würfeln beträgt jeweils 1/6; die Faustformel für $\mu\pm \sigma$ liefert hier also eine gute Näherung. Die Faustformel für $\mu\pm 2\sigma$ passt hingegen nicht, da nicht nur 95 %, sondern 100 % der Würfelergebnisse im Intervall 3,5±3,4 liegen.

Binomialverteilung

Würfelt man 500 Mal mit einem fairen Würfel, so ist die Anzahl der Einser binomialverteilt mit n = 500 und $p=\tfrac{1}{6}$; der Erwartungswert beträgt

$\mu=np=\frac{500}{6}\approx 83{,}3$

und die Standardabweichung

$\sigma = \sqrt{np(1-p)}= \sqrt{ 500 \cdot \frac{1}{6} \cdot \frac{5}{6}}\approx 8{,}3$,

obige Faustformeln lassen also erwarten, dass in 68% der Fälle die Anzahl der Einser zwischen 75 und 92 liegt und in 95% der Fälle zwischen 67 und 100.

Schätzung der Standardabweichung der Grundgesamtheit aus einer Stichprobe

Allgemeiner Fall

Berechnungsgrundlagen

Sind die n Zufallsvariablen X_i unabhängig und identisch verteilt, also beispielsweise eine Stichprobe, so wird die Standardabweichung der Grundgesamtheit der Stichprobe häufig mit der Formel

$S = \sqrt{S^2} := \sqrt{\frac{1}{n-1} \sum_{i=1}^n{(X_i-\bar{X})^2}}$

geschätzt. Dabei ist

• S die Schätzfunktion für die Standardabweichung σ_X der Grundgesamtheit
• n der Stichprobenumfang (Anzahl der Werte)
• X_i die Merkmalsausprägungen am i-ten Element der Stichprobe
• $\bar{X}= \frac{1}{n} \sum_{i=1}^n{X_i}$ der empirische Mittelwert, also das arithmetische Mittel der Stichprobe.

Diese Formel erklärt sich daraus, dass die korrigierte Stichprobenvarianz S² ein erwartungstreuer Schätzer für die Varianz $\sigma_X^2$ der Grundgesamtheit ist. Im Gegensatz dazu ist aber S kein erwartungstreuer Schätzer für die Standardabweichung. Da die Quadratwurzel eine konkave Funktion ist, folgt aus der Jensenschen Ungleichung

$\operatorname{E} S = \operatorname{E}\sqrt {S^2} \leq \sqrt{\operatorname{E}\left(S^2 \right)} = \sigma_X$.

Dieser Schätzer unterschätzt also in den meisten Fällen die Standardabweichung der Grundgesamtheit.

Beispiel

Wählt man eine der Zahlen − 1 oder + 1 durch Wurf einer fairen Münze, also beide mit Wahrscheinlichkeit jeweils $\tfrac 12$, so ist das eine Zufallsgröße mit Erwartungswert 0, Varianz σ² = 1 und Standardabweichung σ = 1. Berechnet man aus n = 2 unabhängigen Würfen X₁ und X₂ die korrigierte Stichprobenvarianz

$S^2=\frac 1{2-1}\left(\left(X_1-\bar X\right)^2+\left(X_2-\bar X\right)^2\right),$

wobei

$\bar X=\frac{X_1+X_2}2$

den Stichprobenmittelwert bezeichnet, so gibt es vier mögliche Versuchsausgänge, die alle jeweils Wahrscheinlichkeit 1 / 4 haben:

X1	X2	$\bar{X}$	S2	S
− 1	− 1	− 1	0	0
− 1	+ 1	0	2	$\sqrt{2}$
+ 1	− 1	0	2	$\sqrt 2$
+ 1	+ 1	+ 1	0	0

Der Erwartungswert der korrigierten Stichprobenvarianz beträgt daher

$\operatorname{E}S^2 = \frac{0+2+2+0}4 = 1 = \sigma^2$

Die korrigierte Stichprobenvarianz ist demnach also tatsächlich erwartungstreu. Der Erwartungswert der korrigierten Stichprobenstandardabweichung beträgt hingegen

$\operatorname{E}S= \frac{0 + \sqrt 2 + \sqrt 2 + 0}4 = \frac{\sqrt 2}2 < 1 = \sigma,$

Die korrigierte Stichprobenstandardabweichung unterschätzt also die Standardabweichung der Grundgesamtheit.

Normalverteilte Zufallsgrößen

Berechnungsgrundlagen

Für den Fall normalverteilter Zufallsgrößen lässt sich allerdings ein erwartungstreuer Schätzer angeben:^[2]

$\hat{\sigma} = \sqrt{\frac{N-1}{2}} \ \frac{\Gamma\left(\frac{N-1}{2}\right)} {\Gamma\left(\frac{N}{2}\right)} \ s_X$

Dabei ist

• $\hat{\sigma}$ die erwartungstreue Schätzung der Standardabweichung und
• Γ(x) die Gammafunktion.

Korrekturfaktoren für die erwartungstreue Schätzung der Standardabweichung

Stichprobenumfang	Korrekturfaktor
2	1,253314
5	1,063846
10	1,028109
15	1,018002
25	1,010468

Beispiel

Es wurden bei einer Stichprobe aus einer normalverteilten Zufallsgröße die fünf Werte 3, 4, 5, 6, 7 gemessen. Man soll nun die Schätzung für die Standardabweichung errechnen.

Der Stichprobenvarianz ist:

$s_X^2=\tfrac 14(2^2+1^2+0+1^2+2^2)=2{,}5$

Der Korrekturfaktor ist in diesem Fall

$\sqrt{2} \ \frac{\Gamma\left(2\right)}{\Gamma\left(2{,}5\right)} \approx 1{,}063846$

und die erwartungstreue Schätzung für die Standardabweichung ist damit näherungsweise

$\hat{\sigma} =1{,}064 \sqrt{2{,}5}=1{,}68$

Maximum-Likelihood-Schätzung für die Standardabweichung einer Normalverteilung

Die eindimensionale Normalverteilung kann unter anderem so dargestellt werden, dass die Standardabweichung ein Parameter der Verteilung ist. Bei dieser Schätzung kann die Eigenschaft der Maximum-Likelihood-Schätzung genutzt werden, dass eine monotone Transformation einer Maximum-Likelihood-Schätzung eine Maximum-Likelihood-Schätzung für die monotone Transformation des geschätzten Parameters ist. Das bedeutet, dass die Quadratwurzel einer Maximum-Likelihood-Schätzung eines Parameters, der nur positiv sein kann, eine Maximum-Likelihood-Schätzung für die Quadratwurzel dieses Parameters ist.

$\hat{\sigma}_{\rm ML} = \sqrt {\frac{1}{n} \sum_{i=1}^n{(x_i-\bar{x})^2}}$

Diese Schätzung ist eine Maximum-Likelihood-Schätzung für einen Parameter der Normalverteilung oder für eine Transformation dieses Parameters. Sie ist nicht auf die Schätzung der Standardabweichung einer beliebigen Verteilung zu übertragen.

Die Maximum-Likelihood-Schätzung für die Standardabweichung einer Poisson-Verteilung ist beispielsweise die Quadratwurzel aus dem arithmetischen Mittel.

Als Maximum-Likelihood-Schätzung für die Standardabweichung aus der Stichprobe {3, 4, 5, 6, 7} erhält man also

$\hat{\sigma}_{\rm ML} = \sqrt {\frac{1}{5} \cdot 10} = \sqrt{2} \approx 1{,}414$

unter der Voraussetzung, dass wir $\bar{x}$ schätzen mit

$\bar{x}=\frac{1}{n}\sum_{i=1}^n{x_i}$

Berechnung für auflaufende Messwerte

In Systemen, die kontinuierlich große Mengen an Messwerten erfassen, ist es oft unpraktisch, alle Messwerte zwischenzuspeichern, um die Standardabweichung zu berechnen.

In diesem Zusammenhang ist es günstiger, eine modifizierte Formel zu verwenden, die den kritischen Term $\sum_{i=1}^n{(x_i-\bar{x})^2}$ umgeht. Dieser kann nicht für jeden Messwert sofort berechnet werden, da der Mittelwert $\bar{x}$ nicht konstant ist.

Durch Anwendung des Verschiebungssatzes und der Definition des Mittelwerts $\bar{x} = \frac{1}{n}\sum_{i=1}^n{x_i}$ gelangt man zur Darstellung

$\begin{align} s & = {} \sqrt{\frac{1}{n-1} \left[\left(\sum_{i=1}^n x_i^2\right) - \frac{1}{n}\left(\sum_{i=1}^n x_i\right)^2\right]} \end{align}$

die sich für jeden eintreffenden Messwert sofort aktualisieren lässt, wenn die Summe der Messwerte $\sum_{i=1}^n{x_i}$ sowie die Summe ihrer Quadrate $\sum_{i=1}^n{x_i^2}$ mitgeführt und fortlaufend aktualisiert werden. Diese Darstellung ist allerdings numerisch weniger stabil, insbesondere kann der Term unter der Quadratwurzel numerisch durch Rundungsfehler kleiner als 0 werden.

Ein analoger Algorithmus wird von Donald Ervin Knuth in The Art of Computer Programming beschrieben. ^[3]

Weblinks

 Wiktionary: Standardabweichung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

 Commons: Standardabweichung – Album mit Bildern und/oder Videos und Audiodateien

 Wikibooks: Beispielprogramm Mittelwert und Standardabweichung in Gambas / Basic – Lern- und Lehrmaterialien

• Filmclip Mittelwert und Standardabweichung
• Standard Deviation (englisch)

Einzelnachweise

1. ↑ Mareke Arends: Epidemiologie bulimischer Symptomatik unter 10-Klässlern in der Stadt Halle. Dissertation zur Erlangung des akademischen Grades Doktor der Medizin (Dr. med.) vorgelegt an der Medizinischen Fakultät der Martin-Luther-Universität Halle-Wittenberg, 2005. Tabelle 9, S 30.
2. ↑ Weisstein, Eric W. "Standard Deviation Distribution." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/StandardDeviationDistribution.html
3. ↑ Donald E. Knuth: The Art of Computer Programming. Volume 2: Seminumerical Algorithms. 3A Auflage. Addison-Wesley Longman, Amsterdam 4. November 1997, ISBN 0-201-89684-2.