- Perfekter Körper
-
In der abstrakten Algebra ist ein Unterkörper eines Körpers L eine Teilmenge
 , die 0 und 1 enthält und mit den auf K eingeschränkten Verknüpfungen selbst ein Körper ist. L wird dann Oberkörper von K genannt. Das Paar L und K bezeichnet man als Körpererweiterung und schreibt es als L / K oder L | K, seltener als L:K.
, die 0 und 1 enthält und mit den auf K eingeschränkten Verknüpfungen selbst ein Körper ist. L wird dann Oberkörper von K genannt. Das Paar L und K bezeichnet man als Körpererweiterung und schreibt es als L / K oder L | K, seltener als L:K.Zum Beispiel ist der Körper
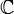 der komplexen Zahlen ein Oberkörper des Körpers
der komplexen Zahlen ein Oberkörper des Körpers 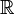 der reellen Zahlen.
der reellen Zahlen.Inhaltsverzeichnis
Definition und Schreibweisen
Sei L ein Körper, und sei K eine Teilmenge von L, die 0 und 1 enthält (die beiden neutralen Elemente) und mit den auf K eingeschränkten Verknüpfungen Addition und Multiplikation selbst ein Körper ist. In diesem Fall heißt K Unterkörper (oder Teilkörper) von L und L heißt Oberkörper (oder Erweiterungskörper) von K.
Eine Teilmenge
 ist genau dann ein Teilkörper von L, wenn sie 0 und 1 enthält und bezüglich der vier Verknüpfungen Addition, Multiplikation, Negation (d. h. Übergang von x zu -x) und Kehrwertbildung (d. h. Übergang von x zu 1/x) abgeschlossen ist, d.h. die Verknüpfung von Elementen von K liefert wieder ein Element von K.
ist genau dann ein Teilkörper von L, wenn sie 0 und 1 enthält und bezüglich der vier Verknüpfungen Addition, Multiplikation, Negation (d. h. Übergang von x zu -x) und Kehrwertbildung (d. h. Übergang von x zu 1/x) abgeschlossen ist, d.h. die Verknüpfung von Elementen von K liefert wieder ein Element von K.Die verbreitetste Schreibweise für Körpererweiterungen ist L / K (nicht als Bruch, sondern nebeneinander mit Schrägstrich), manchmal findet man auch L | K, seltener die Schreibweise L:K. Einige Autoren schreiben auch lediglich
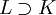 und fügen in Worten an, dass es sich um eine Körpererweiterung handelt.
und fügen in Worten an, dass es sich um eine Körpererweiterung handelt.Die Schreibweise L / K entspricht am ehesten der Sprechweise "L über K", es besteht aber eine geringe Verwechslungsgefahr mit Faktorstrukturen wie Faktorgruppen oder Faktorräumen, die ebenfalls mit einem Schrägstrich geschrieben werden.
Etwas allgemeiner betrachtet man auch den folgenden Fall als Körpererweiterung: Seien K, K' und L Körper, K' Teilkörper von L und K isomorph zu K' . Wenn es nicht zu Missverständnissen führt, identifiziert man K und K' , und fasst so K selbst als Teilkörper von L auf. Dies kommt daher, dass man in der Körpertheorie isomorphe Körper häufig nicht unterscheidet, da sie sich in vielen Belangen gleich verhalten.
Ein Körper M heißt Zwischenkörper der Körpererweiterung L/K, wenn M ein Unterkörper von L und ein Oberkörper von K ist, also
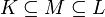 gilt.
gilt.
Sei im folgenden stets L/K eine Körpererweiterung.Erweiterungsgrad
Man kann L als Vektorraum über K auffassen, wobei die Vektoraddition die Körper-Addition in L ist und die Skalarmultiplikation die Körper-Multiplikation von Elementen aus L mit Elementen aus K. Die Dimension dieses Vektorraums nennt man den Grad der Erweiterung, und schreibt ihn als [L : K]. Die Erweiterung heißt endlich oder unendlich, je nachdem ob der Grad endlich oder unendlich ist.
Ein Beispiel für eine endliche Körpererweiterung ist die Erweiterung
 der reellen Zahlen zu den komplexen Zahlen. Der Grad
der reellen Zahlen zu den komplexen Zahlen. Der Grad ![[\C : \R]](/pictures/dewiki/49/19fa2c6d36bc78904013d1863aa5b488.png) dieser Erweiterung ist 2, da {1,i} eine
dieser Erweiterung ist 2, da {1,i} eine 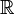 -Basis von
-Basis von 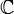 ist. Im Gegensatz dazu ist
ist. Im Gegensatz dazu ist ![[\R : \Bbb Q] = \infty](/pictures/dewiki/54/67d95c746999846ac1aa01f176106707.png) (genauer gleich der Mächtigkeit c des Kontinuums), also ist diese Erweiterung unendlich.
(genauer gleich der Mächtigkeit c des Kontinuums), also ist diese Erweiterung unendlich.Sind M/L und L/K Körpererweiterungen, dann ist auch M/K eine Körpererweiterung, und es gilt der Gradsatz
![[M : K] = [M : L] \cdot [L : K]](/pictures/dewiki/51/3982bb3aa1046ff9602ed60705d19b88.png) .
.
Dies gilt auch im Falle unendlicher Erweiterungen (als Gleichung von Kardinalzahlen, oder alternativ mit den üblichen Rechenregeln für das Symbol unendlich). L/K heißt dabei eine Teilerweiterung von M/K.
Algebraisch und transzendent
Ein Element l von L, das Nullstelle eines Polynoms über K ist, heißt algebraisch über K. Das normierte Polynom von kleinstem Grad mit dieser Nullstelleneigenschaft heißt Minimalpolynom von l. Ist ein Element nicht algebraisch, dann heißt es transzendent. Der Fall L = C und K = Q ist dabei besonders wichtig. Siehe dazu algebraische Zahl, transzendente Zahl.
Ist jedes Element von L algebraisch über K, dann heißt L/K algebraische Erweiterung, andernfalls transzendente Erweiterung. Wenn jedes Element von L\K transzendent ist, dann heißt die Erweiterung rein transzendent.
Man kann zeigen, dass eine Erweiterung genau dann algebraisch ist, wenn sie die Vereinigung aller ihrer endlichen Teilerweiterungen ist. Damit ist jede endliche Erweiterung algebraisch; zum Beispiel trifft dies für
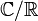 zu. Die Körpererweiterung
zu. Die Körpererweiterung 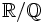 ist dagegen transzendent, wenn auch nicht rein transzendent. Es gibt aber auch unendliche algebraische Erweiterungen, zum Beispiel den algebraischen Abschluss von
ist dagegen transzendent, wenn auch nicht rein transzendent. Es gibt aber auch unendliche algebraische Erweiterungen, zum Beispiel den algebraischen Abschluss von  .
.Körperadjunktion
Ist V eine Teilmenge von L, dann ist der Körper K(V) ("K adjungiert V") definiert als der kleinste Teilkörper von L, der K und V enthält, mit anderen Worten, der Durchschnitt aller K und V enthaltenden Teilkörper von L. K(V) besteht aus allen Elementen von L, die mit endlich vielen Verknüpfungen
 aus den Elementen von K und V gebildet werden können. Ist L = K(V), dann sagt man, L wird von V erzeugt.
aus den Elementen von K und V gebildet werden können. Ist L = K(V), dann sagt man, L wird von V erzeugt.Primkörper
Der Primkörper eines Körpers K ist der Durchschnitt aller Unterkörper von K. Als Primkörper bezeichnet man auch einen Körper K, der keine echten Teilkörper hat, der also selbst sein eigener Primkörper ist.
Jeder Primkörper ist zum Körper
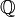 der rationalen Zahlen oder einem der Restklassenkörper
der rationalen Zahlen oder einem der Restklassenkörper 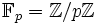 isomorph (wobei p eine Primzahl ist).
isomorph (wobei p eine Primzahl ist).Falls der Primkörper von K isomorph zu
 ist, so sagt man, er habe Charakteristik null. Ist der Primkörper von K isomorph zu
ist, so sagt man, er habe Charakteristik null. Ist der Primkörper von K isomorph zu 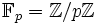 , so sagt man er habe Charakteristik p.
, so sagt man er habe Charakteristik p.Einfache Erweiterung
Eine Körpererweiterung K(a)/K, die von einem einzelnen Element a erzeugt wird, heißt einfach. Eine einfache Erweiterung ist endlich, wenn sie von einem algebraischen Element erzeugt wird, und rein transzendent, wenn sie von einem transzendenten Element erzeugt wird. Zum Beispiel ist C eine einfache Erweiterung von R, denn C = R(i) mit i2 = -1. Die Erweiterung R/Q kann nicht einfach sein, da sie weder algebraisch noch rein transzendent ist. Jede endliche Erweiterung von Q ist einfach. Allgemeiner gilt: Jede endliche Erweiterung eines Körpers mit Charakteristik 0 ist eine einfache Erweiterung.
Kompositum
Sind K1 und K2 beide Teilkörper von L, dann heißt der kleinste gemeinsame Oberkörper K1(K2) = K2(K1) das Kompositum von K1 und K2.
Sind K1 und K2 beide endlich erweiterte Oberkörper von K, dann ist auch K1(K2)/K endlich.
Normale Erweiterungen
L/K heißt normale Erweiterung, wenn alle Minimalpolynome über K von Elementen aus L in L vollständig in Linearfaktoren zerfallen. Ist a in L und f sein Minimalpolynom über K, dann heißen die Nullstellen von f in L die Konjugierten von a. Sie sind genau die Bilder von a unter K-Automorphismen von L.
Ist L nicht normal über K, dann gibt es jedoch einen Oberkörper von L, der normal über K ist. Er heißt die normale Hülle von L/K.
Ein Beispiel für eine nicht normale Körpererweiterung ist
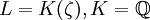 mit
mit ![\zeta = \sqrt[3]{2}\in\mathbb{R}](/pictures/dewiki/98/b5a273f6eafa922f0267e3657f459d2d.png) : Das Minimalpolynom des erzeugenden Elements ist X3 − 2 und hat komplexe, also nicht in L liegende, Nullstellen.
: Das Minimalpolynom des erzeugenden Elements ist X3 − 2 und hat komplexe, also nicht in L liegende, Nullstellen.Zerfällungskörper
Der Zerfällungskörper eines Polynoms ist eine spezielle Körpererweiterung.
K sei weiterhin ein Körper,
![p \in K[X]](/pictures/dewiki/48/0891c2120b8ca550c6b5158e547991d0.png) ein nicht konstantes Polynom über K. L/K ist ein Zerfällungskörper von p, wenn alle Nullstellen von p in L liegen und L diesbezüglich minimal ist. Man sagt auch, dass L durch Adjunktion aller Wurzeln von p an K entsteht. Dieser Körper heißt Zerfällungskörper, da p über L in Linearfaktoren zerfällt. Jedes nicht konstante Polynom besitzt einen bis auf Isomorphie eindeutigen Zerfällungskörper.
ein nicht konstantes Polynom über K. L/K ist ein Zerfällungskörper von p, wenn alle Nullstellen von p in L liegen und L diesbezüglich minimal ist. Man sagt auch, dass L durch Adjunktion aller Wurzeln von p an K entsteht. Dieser Körper heißt Zerfällungskörper, da p über L in Linearfaktoren zerfällt. Jedes nicht konstante Polynom besitzt einen bis auf Isomorphie eindeutigen Zerfällungskörper.Zerfällungskörper sind stets normale Erweiterungen, und umgekehrt ist jede endliche normale Erweiterung Zerfällungskörper eines nicht konstanten Polynoms über dem Grundkörper.
Zum Beispiel hat
![X^3-2 \in \mathbb{Q}[X]](/pictures/dewiki/102/f776a93c97a5d016ebd8235ffe2a2a58.png) den Zerfällungskörper
den Zerfällungskörper ![\mathbb{Q}(\sqrt[3]{2},e^\frac{2\pi i}{3}).](/pictures/dewiki/54/6fe507a8d8d663df50298b02710b2fed.png)
Separabilität
Separable Polynome
Ein Polynom f über K heißt separabel, wenn es in seinem Zerfällungskörper nur einfache Nullstellen hat. Es ist genau dann separabel, wenn es teilerfremd zu seiner formalen Ableitung f' ist. Ist f irreduzibel, dann ist es separabel genau dann wenn f' nicht das Nullpolynom ist.
Es gibt aber auch eine abweichende Definition, derzufolge ein Polynom separabel heißt, wenn jeder seiner irreduziblen Teiler im obigen Sinn separabel ist. Für irreduzible Polynome und damit insbesondere für Minimalpolynome stimmen beide Definitionen überein, für reduzible Polynome unterscheiden sie sich jedoch.
Separable Erweiterungen
Ein algebraisches Element von L heißt separabel über K, wenn sein Minimalpolynom über K separabel ist. Eine algebraische Erweiterung L / K heißt separable Erweiterung, wenn alle Elemente von L separabel sind.
Ein Beispiel für eine inseparable Körpererweiterung ist
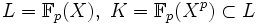 , denn das Minimalpolynom
, denn das Minimalpolynom ![T^p-X^p\in K[T]](/pictures/dewiki/52/499e181c044761aef808466a16a892b7.png) des Erzeugers X zerfällt bereits über L in (T − X)p.
des Erzeugers X zerfällt bereits über L in (T − X)p.Der Separabilitätsgrad [L:K]s einer algebraischen Körpererweiterung L / K wird definiert als die Anzahl der K-Homomorphismen von L in den L enthaltenden algebraischen Abschluss von K, die auf K die Identität sind. Für L = K(a) und ein Minimalpolynom f von a über K ist [L:K]s die Anzahl der verschiedenen Nullstellen von f im algebraischen Abschluss von K. Für einen Turm algebraischer Körpererweiterungen M / L / K gilt die Produktformel
![[M:K]_s=[M:L]_s\cdot [L:K]_s](/pictures/dewiki/99/ca7af43cd8467acad39e4097877dcc66.png) .
.Vollkommene Körper
Für viele Körper K, über denen Körpererweiterungen untersucht werden, sind irreduzible Polynome immer separabel und man muss sich bei diesen Körpern nicht um die Bedingung der Separabilität kümmern. Man nennt diese Körper vollkommen oder perfekt.
Etwas formaler kann ein vollkommener Körper durch eine der folgenden gleichwertigen Eigenschaften des Körpers K bzw. des Polynomrings K[X] charakterisiert werden:
- Jedes irreduzible Polynom in K[X] ist separabel.
- Jeder algebraische Abschluss
 von K ist eine Galoiserweiterung (im weiteren Sinn, der im Artikel Galoisgruppe erläutert wird: auch unendlichdimensionale Erweiterungen können Galoiserweiterungen sein) von K.
von K ist eine Galoiserweiterung (im weiteren Sinn, der im Artikel Galoisgruppe erläutert wird: auch unendlichdimensionale Erweiterungen können Galoiserweiterungen sein) von K. - Jede algebraische Körpererweiterung von K ist separabel über K.
- Der Körper K hat entweder die Charakteristik 0 oder er hat Primzahlcharakteristik p und es gilt K = Kp, d. h., der Frobeniusendomorphismus ist bijektiv.
- Der Körper K hat entweder die Charakteristik 0 oder er hat Primzahlcharakteristik p und jedes Element aus K hat eine pte Wurzel.
Insbesondere sind Körper der Charakteristik 0, endliche Körper und algebraisch abgeschlossene Körper vollkommen. Ein Beispiel für einen nicht vollkommenen Körper ist
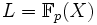 – dort hat das Körperelement X keine pte Wurzel.
– dort hat das Körperelement X keine pte Wurzel.K-Automorphismen
Die Gruppe
 aller Automorphismen von L nennt man die Automorphismengruppe von L .
aller Automorphismen von L nennt man die Automorphismengruppe von L .Für jeden Automorphismus
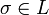 definiert man den Fixkörper
definiert man den Fixkörper 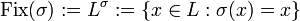 aller Elemente von L, die von s festgehalten werden. Man rechnet leicht nach, dass das ein Teilkörper von L ist. Der Fixkörper Fix(G) (auch geschrieben als LG) einer ganzen Gruppe G von Automorphismen in L ist definiert durch:
aller Elemente von L, die von s festgehalten werden. Man rechnet leicht nach, dass das ein Teilkörper von L ist. Der Fixkörper Fix(G) (auch geschrieben als LG) einer ganzen Gruppe G von Automorphismen in L ist definiert durch:

Die Automorphismen von L, die mindestens K punktweise fest lassen, bilden eine Untergruppe von Aut(L), die Gruppe der K-Automorphismen von L, bezeichnet als
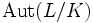 oder auch
oder auch 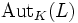 .
.Galoiserweiterung
Ist die Erweiterung L/K algebraisch, normal und separabel, dann heißt die Erweiterung galoissch ([ɡaloaːʃ], nach Évariste Galois). Eine algebraische Erweiterung ist genau dann galoissch, wenn der Fixkörper Fix(Aut(L/K)) der K-Automorphismengruppe gleich K ist.
Man nennt Aut(L/K) in diesem Fall die Galoisgruppe der Erweiterung und schreibt sie als
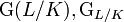 , oder
, oder 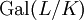 . Abweichend von der im vorliegenden Artikel benutzten Sprachregelung wird im Artikel „Galoisgruppe“ die Gruppe Aut(L/K) stets als Galoisgruppe bezeichnet, auch wenn die Erweiterung L/K nicht galoissch ist.
. Abweichend von der im vorliegenden Artikel benutzten Sprachregelung wird im Artikel „Galoisgruppe“ die Gruppe Aut(L/K) stets als Galoisgruppe bezeichnet, auch wenn die Erweiterung L/K nicht galoissch ist.Ist die Galoisgruppe einer Galoiserweiterung abelsch, dann heißt diese abelsche Erweiterung, ist sie zyklisch, dann heißt die Erweiterung zyklisch. Zum Beispiel ist
 abelsch und zyklisch, denn ihre Galoisgruppe ist zweielementig und besteht aus der Identität und der komplexen Konjugation. Die Erweiterung
abelsch und zyklisch, denn ihre Galoisgruppe ist zweielementig und besteht aus der Identität und der komplexen Konjugation. Die Erweiterung  ist nicht galoissch, denn der einzige Automorphismus von
ist nicht galoissch, denn der einzige Automorphismus von 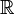 ist die Identität, und die lässt offensichtlich mehr als nur
ist die Identität, und die lässt offensichtlich mehr als nur 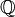 fest – freilich ist die Erweiterung schon deshalb nicht galoissch, weil sie nicht algebraisch ist.
fest – freilich ist die Erweiterung schon deshalb nicht galoissch, weil sie nicht algebraisch ist.Für weitere Informationen über Galoiserweiterungen siehe den Artikel Galoistheorie.
Beispiele
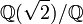 ist eine Galoiserweiterung. Die Automorphismengruppe besteht genau aus der Identität und dem Automorphismus, der
ist eine Galoiserweiterung. Die Automorphismengruppe besteht genau aus der Identität und dem Automorphismus, der  konstant lässt, aber
konstant lässt, aber 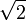 und
und  vertauscht. Der Fixkörper davon ist
vertauscht. Der Fixkörper davon ist  .
.![\mathbb{Q}( \sqrt[3]{2} )/\mathbb{Q}](/pictures/dewiki/97/ad7adb2b9452a3be4ecd2fd1835f83b0.png) ist keine Galoiserweiterung, denn die Automorphismengruppe A besteht nur aus der Identität. Ein Automorphismus auf dieser Erweiterung, der
ist keine Galoiserweiterung, denn die Automorphismengruppe A besteht nur aus der Identität. Ein Automorphismus auf dieser Erweiterung, der ![\ \sqrt[3]{2}\](/pictures/dewiki/55/7a7649042dda2a27d9be646ba90e14ba.png) nicht fix lässt, müsste
nicht fix lässt, müsste ![\ \sqrt[3]{2}\](/pictures/dewiki/55/7a7649042dda2a27d9be646ba90e14ba.png) auf eine andere dritte Wurzel aus 2 abbilden, jedoch enthält
auf eine andere dritte Wurzel aus 2 abbilden, jedoch enthält ![\mathbb{Q}( \sqrt[3]{2} )](/pictures/dewiki/49/134768b82d8e75ae966ef47c04fc31f8.png) keine weiteren dritten Wurzeln aus 2. Da es sich um keine Galoiserweiterung handelt, heißt sie auch weder abelsch noch zyklisch, obwohl die Gruppe A (als triviale Gruppe) natürlich zyklisch und abelsch ist.
keine weiteren dritten Wurzeln aus 2. Da es sich um keine Galoiserweiterung handelt, heißt sie auch weder abelsch noch zyklisch, obwohl die Gruppe A (als triviale Gruppe) natürlich zyklisch und abelsch ist.
Konstruierbarkeitsfragen
Die klassischen Probleme der antiken Mathematik, bei denen es um die Konstruierbarkeit einer bestimmten Zahl (als Streckenlänge) allein mit Zirkel und Lineal aus rationalen Zahlen geht, konnten mit der Galoistheorie in gruppentheoretische Fragen umformuliert werden. Mit dem Grundgedanken von René Descartes, dass die Punkte auf Geraden (Lineal) und Kreisen (Zirkel) durch analytische Gleichungen darstellbar sind, lässt sich zeigen, dass die konstruierbaren Zahlen (Koordinaten von endlichen Schnittmengen von zwei dieser Figuren in der rationalen Zahlenebene bzw. auf der Basis bereits konstruierter Zahlen) genau die folgenden sind:
- Die rationalen Zahlen,
- die Quadratwurzeln aus konstruierbaren Zahlen,
- Summe, Differenz und Produkt von zwei konstruierbaren Zahlen,
- der Kehrwert jeder von 0 verschiedenen konstruierbaren Zahl.
Damit kann man zeigen, dass jede konstruierbare reelle Zahl
- algebraisch und
- vom Grad einer Zweierpotenz 2n über dem Körper
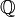 der rationalen Zahlen ist.
der rationalen Zahlen ist.
Dies bedeutet, dass für eine konstruierbare Zahl c die Körpererweiterung
 eine endliche, algebraische Erweiterung vom Grad 2n (
eine endliche, algebraische Erweiterung vom Grad 2n ( ) sein muss. Dies ist noch keine hinreichende Bedingung, genügt aber in den klassischen Fragen für einen Unmöglichkeitsbeweis.
) sein muss. Dies ist noch keine hinreichende Bedingung, genügt aber in den klassischen Fragen für einen Unmöglichkeitsbeweis.- Quadratur des Kreises: Unmöglich, da die Kreiszahl π nicht algebraisch ist.
- Verdoppelung des Würfels: Unmöglich: Im Verhältnis zum konstruierten Ausgangswürfel (etwa ein Würfel mit der Kantenlänge 1) hätte der neue Würfel die Kantenlänge
![\alpha=\sqrt[3]{2}](/pictures/dewiki/97/a26bb75dc8b82a62c9e61b130c8e5056.png) . Die Körpererweiterung
. Die Körpererweiterung 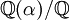 hat den Grad 3 – keine Zweierpotenz.
hat den Grad 3 – keine Zweierpotenz. - Dreiteilung des Winkels: Ein Winkel mit dem Gradmaß 60° kann mit Zirkel und Lineal nicht in drei gleiche Teile geteilt werden. Wäre dieser Winkel – also 20° – konstruierbar, dann könnte man auch die reelle Zahl
 konstruieren. Für jeden Winkel α gilt das Additionstheorem cos(3α) = 4(cos(α))3 − 3cos(α). Also löst unsere Zahl ξ die Gleichung
konstruieren. Für jeden Winkel α gilt das Additionstheorem cos(3α) = 4(cos(α))3 − 3cos(α). Also löst unsere Zahl ξ die Gleichung
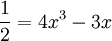 und ist daher eine Nullstelle von
und ist daher eine Nullstelle von- 8x3 − 6x − 1. Da dieses Polynom über
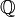 irreduzibel ist, hat ξ über
irreduzibel ist, hat ξ über 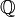 den Grad 3.
den Grad 3.
Literatur
- Thomas W. Hungerford: Algebra. 5. print. Springer-Verlag, 1989, ISBN 0-387-90518-9
Wikimedia Foundation.
