Frobeniusautomorphismus

In der Algebra bezeichnet der Begriff Frobeniushomomorphismus (auch Frobeniusmorphismus oder kurz Frobenius, nach dem deutschen Mathematiker Ferdinand Georg Frobenius) einen Endomorphismus von Ringen der Charakteristik p.

Definition:

Sei R ein kommutativer Ring der Charakteristik p > 0 prim. Dann ist der Frobenius 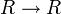$R \rightarrow R$ definiert durch $x \mapsto x^p$.

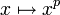Eigenschaften:

Der Frobenius ist ein Ringhomomorphismus, die Verträglichkeit mit der Addition ist wegen der (sogenannten "falschen") binomischen Formel in Charakteristik p ( (a + b)^p = a^p + b^p ) gegeben.

Beispiele

• Eine Potenz des Frobenius ist der Erzeuger der Galoisgruppe einer endlichen Galoiserweiterung eines endlichen Körpers.
• Ist der Frobenius eines Körpers surjektiv (äquivalent: Das Ziehen von p-ten Wurzel aus jedem Körperelement ist möglich), dann ist der Körper perfekt.
• In der algebraischen Geometrie ist der absolute Frobenius eines Schemas der Charakteristik p definiert als Identität auf dem topologischen Raum und p-Potenzierung auf der Strukturgarbe.
• Auf einem affinen Schema ist der absolute Frobenius durch den Frobenius des zugrundeliegenden Ringes gegeben.