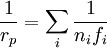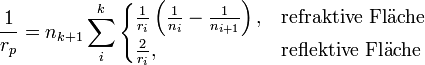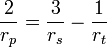Petzval-Bedingung — Pẹtzval Bedingung [ val], Pẹtzval Summe, Optik: von J. Petzval 1843 formulierte Bedingung für ein optisches System, bei deren Erfüllung im seidelschen Gebiet ein ebenes Bildfeld entsteht (korrigierte Bildfeldwölbung). Die Petzval Bedingung… … Universal-Lexikon
Petzval — Joseph Petzval Jozef Maximilián Petzval, auch: deutsch Josef Maximilian Petzval oder ungarisch: Petzval József (oder Józeph) Miksa, (* 6. Januar 1807 in Spišská Belá (dt. Zipser Bela, ung. Szepesbéla); † 19. September 1891 in Wien) war ein… … Deutsch Wikipedia
Petzval-Fläche — Die Petzval Summe bzw. der daraus resultierende Radius der Petzval Fläche beschreibt die Bildfeldwölbung eines optischen Systems. Sie wurde von Josef Maximilian Petzval entwickelt und 1843 publiziert. Für eine Anzahl dünner Linsen mit der… … Deutsch Wikipedia
Petzval-Summe — Die Petzval Summe bzw. der daraus resultierende Radius der Petzval Fläche beschreibt die Bildfeldwölbung eines optischen Systems. Sie wurde von Josef Maximilian Petzval entwickelt und 1843 publiziert. Für eine Anzahl dünner Linsen mit der… … Deutsch Wikipedia
Petzval-Transformation — Die Laplace Transformation (benannt nach Pierre Simon Laplace) ist eine einseitige Integraltransformation, die eine gegebene Funktion f(t) vom reellen Zeitbereich (t = Zeit) in eine Funktion F(s) im komplexen Spektralbereich (Frequenzbereich;… … Deutsch Wikipedia
Josef Petzval — Joseph Petzval Jozef Maximilián Petzval, auch: deutsch Josef Maximilian Petzval oder ungarisch: Petzval József (oder Józeph) Miksa, (* 6. Januar 1807 in Spišská Belá (dt. Zipser Bela, ung. Szepesbéla); † 19. September 1891 in Wien) war ein… … Deutsch Wikipedia
Josef Maximilian Petzval — Joseph Petzval, Lithographie von Adolf Dauthage, 1854 Jozef Maximilián Petzval, auch: deutsch Josef Maximilian Petzval oder ungarisch: Petzval József (oder Józeph) Miksa, (* 6. Januar 1807 in Spišská Belá (dt. Zipser Bela, ung. Szepesbéla); † 19 … Deutsch Wikipedia
Bildfeld — Bildfeld, bei der Abbildung durch ein optisches System der vom Blendenbild der Feldblende (Austrittsluke) scharf begrenzte Teil der Bildfläche beziehungsweise ebene, dem objektseitig das Gesichtsfeld entspricht. Das Bildfeld ist bei einfachen… … Universal-Lexikon
seidelsches Gebiet — seidelsches Gebiet, Optik: der sich an das paraxiale Gebiet anschließende (enge) Bereich um die optische Achse eines abbildenden optischen Systems. Im seidelschen Gebiet gilt die von L. P. von Seidel entwickelte Abbildungsfehlertheorie 3.… … Universal-Lexikon
Laplacetransformation — Die Laplace Transformation (benannt nach Pierre Simon Laplace) ist eine einseitige Integraltransformation, die eine gegebene Funktion f(t) vom reellen Zeitbereich (t = Zeit) in eine Funktion F(s) im komplexen Spektralbereich (Frequenzbereich;… … Deutsch Wikipedia