- Pivot-Verfahren
-
Pivotverfahren nennt sich jeder Algorithmus zur Aufgabenlösung der Linearen Optimierung, der dem unten beschriebenen Pivotansatz folgt. Wichtige Pivotverfahren sind die Simplex-Verfahren[1] und die Criss-Cross-Verfahren[2].
Inhaltsverzeichnis
Pivotansatz
Jedes System linearer Ungleichungen und jedes Lineare Optimierungsproblem lässt sich in folgende, englisch dictionary genannte[1] Grundform bringen:
Diese Darstellung soll aussagen, dass eine Lösung in den Unbekannten
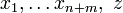 gesucht wird, welche die obige Gleichungen beziehungsweise Ungleichungen erfüllt und dabei die sogenannte Zielvariable
gesucht wird, welche die obige Gleichungen beziehungsweise Ungleichungen erfüllt und dabei die sogenannte Zielvariable 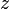 so groß wie möglich wählt.
so groß wie möglich wählt.
Falls nun die Optimalitätsbedingungen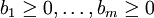 und
und 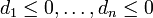 erfüllt sind, kann man eine Lösung für die obige Aufgabe erhalten, indem man die unabhängigen Variablen auf die Werte
erfüllt sind, kann man eine Lösung für die obige Aufgabe erhalten, indem man die unabhängigen Variablen auf die Werte 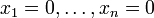 setzt. Zum einen sind die Werte der freigelegten Variablen
setzt. Zum einen sind die Werte der freigelegten Variablen 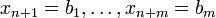 dann nichtnegativ, wie gefordert, zum anderen dürfen sonstige mögliche Lösungen nur unabhängige Variablen mit ebenfalls nichtnegativen Werten enthalten, sodass für jede dieser Lösungen die Ungleichung
dann nichtnegativ, wie gefordert, zum anderen dürfen sonstige mögliche Lösungen nur unabhängige Variablen mit ebenfalls nichtnegativen Werten enthalten, sodass für jede dieser Lösungen die Ungleichung 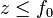 gilt.
gilt.Falls die Optimumbedingungen nicht erfüllt sind, was in der Regel der Fall sein wird, lässt sich das obige lineare Gleichungssystem aber auch andersartig ausdrücken, indem man eine andere, gleichgroße Teilmenge
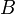 der
der 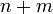 Unbekannten als sogenannte Basisvariablen definiert und diese freilegt. Es sei
Unbekannten als sogenannte Basisvariablen definiert und diese freilegt. Es sei 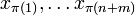 eine neue Anordnung der Unbekannten
eine neue Anordnung der Unbekannten 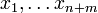 . Dann wählt man die Teilmenge
. Dann wählt man die Teilmengeder Unbekannten als Basis oder Menge der Basisvariablen aus und stellt folgendes neue System auf:
Die Koeffizienten des so abgewandelten Gleichungssystems lassen sich erneut auf die Optimumbedingungen
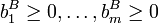 und
und 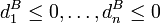 untersuchen, was wiederum unter Umständen zu einer Lösung der Aufgabe führt. Ein Standardergebnis der Linearen Optimierung sagt aus, dass für jede lösbare Aufgabe ein Satz Basisvariablen existiert, der zu einer Lösung führt. Bei erfüllten Optimumbedingungen bilden die Basisvariablen eine sogenannte Optimalbasis des Systems.
untersuchen, was wiederum unter Umständen zu einer Lösung der Aufgabe führt. Ein Standardergebnis der Linearen Optimierung sagt aus, dass für jede lösbare Aufgabe ein Satz Basisvariablen existiert, der zu einer Lösung führt. Bei erfüllten Optimumbedingungen bilden die Basisvariablen eine sogenannte Optimalbasis des Systems.
Jedes nichtverschwindende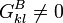 des obigen Gleichungssystems nennt sich Pivotelement, und erlaubt es, die unabhängige Variable
des obigen Gleichungssystems nennt sich Pivotelement, und erlaubt es, die unabhängige Variable 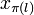 an Stelle der Basisvariablen
an Stelle der Basisvariablen 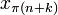 freizulegen, um so weiter nach einer Lösung zu suchen. Das ist die Vorgehensweise eines allgemeinen Pivotverfahrens, wobei aber nicht irgendwelche Pivotelemente gewählt werden, sondern nur sogenannte zulässige Pivots
freizulegen, um so weiter nach einer Lösung zu suchen. Das ist die Vorgehensweise eines allgemeinen Pivotverfahrens, wobei aber nicht irgendwelche Pivotelemente gewählt werden, sondern nur sogenannte zulässige Pivots 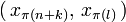 , die folgendes erfüllen müssen:
, die folgendes erfüllen müssen:-
- entweder gilt (a) gleichzeitig
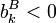 und
und 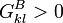 , oder es gilt (b) gleichzeitig
, oder es gilt (b) gleichzeitig 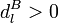 und
und 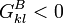
- entweder gilt (a) gleichzeitig
Die Regeln, nach denen in jedem Schritt eines dieser zulässigen Pivotelemente ausgewählt wird, hängen vom jeweiligen Verfahren ab; ein Mindestanspruch ist dabei natürlich, dass das Verfahren nach endlich vielen Schritten anhält, was bei ungeeigneter Auswahl von zulässigen Pivots nicht der Fall ist. Fukuda und Terlaky haben 1999 bewiesen, dass für jede lösbare Aufgabe und für jede Ausgangsbasis eine Folge von maximal
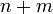 zulässigen Pivots existiert, die zu einer Optimalbasis führt.[3]
zulässigen Pivots existiert, die zu einer Optimalbasis führt.[3]Wie aus der Definition zu ersehen ist, haben Optimalbasen keine zulässigen Pivots, das Verfahren kann in so einem Fall gar nicht fortgeführt werden. Anderseits kann anhand von Argumenten wie im obigen Abschnitt leicht gezeigt werden, dass eine nichtoptimale Basis ohne zulässige Pivots immer zu einer Aufgabe gehört, die keine Lösung hat; entweder, weil das System der Gleichungen und Ungleichungen keine Lösung hat (unzulässige Aufgabe), oder, weil sich Lösungen mit unendlich großem
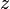 finden lassen (unbeschränkte Aufgabe).
finden lassen (unbeschränkte Aufgabe).Beispiel
In folgendem Beispiel sei
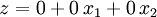 . In diesem Falle wird keine der Variablen maximiert, sondern eine beliebige Lösung in den Unbekannten
. In diesem Falle wird keine der Variablen maximiert, sondern eine beliebige Lösung in den Unbekannten 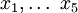 gesucht, die folgende Gleichungen und Ungleichungen erfüllen soll:
gesucht, die folgende Gleichungen und Ungleichungen erfüllen soll:Um Rundungsfehler zu vermeiden, arbeiten wir im folgenden mit rationalen Zahlen und wählen einen gemeinsamen Nenner für sämtliche Einträge. In jedem Schritt wird der zulässige Pivot
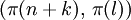 nach folgender Regel gewählt:
nach folgender Regel gewählt:- Wähle
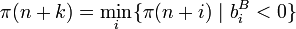 und danach
und danach 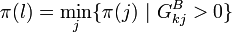 .
.
Für den Fall von
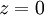 lässt sich beweisen,[2] dass diese einfache (nicht besonders effiziente) Auswahlregel bei jeder lösbaren Aufgabe zu einer Optimalbasis führt.
lässt sich beweisen,[2] dass diese einfache (nicht besonders effiziente) Auswahlregel bei jeder lösbaren Aufgabe zu einer Optimalbasis führt.Die zulässigen Pivots im obigen Gleichungssystem sind
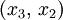 und
und 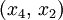 ; wir legen
; wir legen 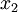 an Stelle von
an Stelle von 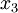 frei und erhalten:
frei und erhalten:Die zulässigen Pivots sind nun
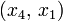 und
und 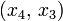 ; wir legen
; wir legen 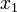 an Stelle von
an Stelle von 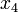 frei und erhalten:
frei und erhalten:Der einzige zulässige Pivot hier ist
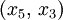 ; wir legen
; wir legen 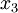 an Stelle von
an Stelle von 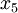 frei und erhalten:
frei und erhalten:Wir erhalten die Lösung:
Kreisanfällige Pivotwahl
Es sei wieder
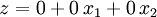 . Bei ungeeigneter Pivotwahl kann ein Pivotverfahren in einen unendlichen Kreislauf oder Endlosschleife geraten. Als Beispiel für eine naheliegende, aber dennoch ungeeignete Pivotwahl betrachten wir folgende Regel, die dem weitverwendeten dualen Simplexverfahren nachempfunden ist:
. Bei ungeeigneter Pivotwahl kann ein Pivotverfahren in einen unendlichen Kreislauf oder Endlosschleife geraten. Als Beispiel für eine naheliegende, aber dennoch ungeeignete Pivotwahl betrachten wir folgende Regel, die dem weitverwendeten dualen Simplexverfahren nachempfunden ist:- Wähle das erste
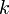 mit
mit 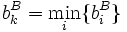 , und danach das erste
, und danach das erste 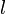 mit
mit 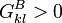 .
.
Wir starten mit dem System:
Wir wählen
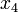 und legt an Stelle dessen
und legt an Stelle dessen 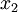 frei (nach der kreissicheren Regel im vorherigen Beispiel hätte man
frei (nach der kreissicheren Regel im vorherigen Beispiel hätte man 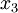 und
und 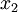 gewählt). Wir erhalten das System:
gewählt). Wir erhalten das System:Wir wählen
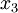 , legen an Stelle dessen
, legen an Stelle dessen 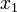 frei und erhalten:
frei und erhalten:Aber dieses Gleichungssystem ist – abgesehen von der Benennung der Veränderlichen – identisch mit dem Startsystem. Die Zahleneinträge des Systems wiederholen sich alle zwei Schritte, nach sechs Schritten wiederholen sich die Gleichungen des Systems in umgestellter Form, und nach insgesamt zwölf Schritten wiederholt sich das Startsystem genau, mit den Gleichungen und Unbekannten am ursprünglichen Ort.
Dualität
Jeder linearen Optimierungsaufgabe lässt sich, von der obigen Grundform abhängig, eine zweite, duale Optimierungsaufgabe zuordnen; die Koeffizientenmatrix dieser sogenannten dualen Aufgabe ist die negative Transposition der Koeffizientenmatrix der ursprünglichen Aufgabe:
(Vorsicht: Bei der Ableitung über diese Formulierung dürfen
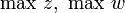 nicht durch
nicht durch 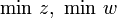 ersetzt werden!)
ersetzt werden!)Die obige Beziehung der Koeffizienten zwischen Primalaufgabe und Dualaufgabe gilt nicht etwa nur für die Ausgangsbasis, sondern bleibt erhalten, solange die Basisvariablen nach denselben Pivots umgewandelt werden:
Daraus folgt, dass jede Optimalbasis der ursprünglichen Aufgabe auch unmittelbar eine Optimalbasis für die duale Aufgabe liefert.
Die Dualitätsbeziehung lässt sich am leichtesten an einem Pivotsystem betrachten, das ausschließlich zwei unabhängige Unbekannte und zwei freigelegte Unbekannte enthält. Man erhält dasselbe System, wenn man zuerst zwei der Unbekannten austauscht und danach die duale Aufgabe herleitet oder wenn man diese Schritte in umgekehrter Reihenfolge tut:![\begin{matrix}
x_i &\!=\!& (~~\alpha) &\!\!\!x_j &\!+\!& (~~\sigma) &\!\!\!x_s \\[6pt]
x_r &\!=\!& (~~\zeta) &\!\!\!x_j &\!+\!& (~~\pi) &\!\!\!x_s
\end{matrix}](/pictures/dewiki/50/22291c73f8dd220714d3c2b08991a41f.png)
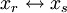
![\begin{matrix}
x_i &\!=\!& (~~{\scriptstyle\alpha}-\frac{\zeta\sigma}{\pi}) &\!\!\!x_j &\!+\!\!& (~~\frac{\sigma}{\pi}) &\!\!\!x_r \\[6pt]
x_s &\!=\!& (~~~-\frac{\zeta}{\pi}~) &\!\!\!x_j &\!+\!\!& (~~\frac{1}{\pi}) &\!\!\!x_r \\
\end{matrix}](/pictures/dewiki/54/628141134bbd03eb39b2828b05f6c635.png)
![-\,[\cdots]^{\,T}](/pictures/dewiki/101/ed00cf108e7d34e090a438b5ef4fd47d.png)
![-\,[\cdots]^{\,T}](/pictures/dewiki/101/ed00cf108e7d34e090a438b5ef4fd47d.png)
![\begin{matrix}
y_j &\!=\!& (-\alpha) &\!\!\!y_i &\!+\!& (-\zeta) &\!\!\!y_r \\[6pt]
y_s &\!=\!& (-\sigma) &\!\!\!y_i &\!+\!& (-\pi) &\!\!\!y_r \\
\end{matrix}](/pictures/dewiki/49/1f3edb15300234f9073de47592a94fb5.png)
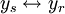
![\begin{matrix}
y_j &\!=\!& (-{\scriptstyle\alpha}+\frac{\zeta\sigma}{\pi}) &\!\!\!y_i &\!+\!\!& (~~\frac{\zeta}{\pi}) &\!\!\!y_s \\[6pt]
y_r &\!=\!& (~~~~-\frac{\sigma}{\pi}~) &\!\!\!y_i &\!+\!\!& (-\frac{1}{\pi}) &\!\!\!y_s \\
\end{matrix}](/pictures/dewiki/97/ac0d9ec8b7fc45214e619f6278fea680.png)
Dieses Schema zeigt auch an, wie sich die Einträge des Pivotsystems von einem Schritt auf den nächsten verändern. Das Zeichen
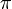 steht für das Pivotelement,
steht für das Pivotelement, 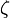 für einen sonstigen Eintrag der Pivotzeile,
für einen sonstigen Eintrag der Pivotzeile, 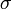 für einen sonstigen Eintrag der Pivotspalte und
für einen sonstigen Eintrag der Pivotspalte und 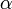 für einen beliebigen Eintrag abseits von Pivotzeile und Pivotspalte. Einträge der Zielbeitragszeile (
für einen beliebigen Eintrag abseits von Pivotzeile und Pivotspalte. Einträge der Zielbeitragszeile (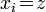 ) und der Basiswertspalte (
) und der Basiswertspalte (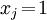 ) werden nach denselben Regeln umgewandelt.
) werden nach denselben Regeln umgewandelt.Beispiel zur Dualität
Die Aufgabe im obigen Beispiel hat folgende duale Aufgabe (die Nullen stammen von
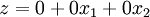 ):
):
Bei der ursprünglichen Aufgabe hatten wir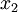 an Stelle von
an Stelle von 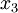 freigelegt. Wenn man im dualen Gleichungssystem
freigelegt. Wenn man im dualen Gleichungssystem 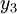 an Stelle von
an Stelle von 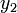 freilegt, erhält man:
freilegt, erhält man:Wenn man nun
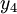 an Stelle von
an Stelle von 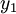 freilegt, erhält man:
freilegt, erhält man:Wenn man
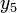 an Stelle von
an Stelle von 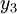 freilegt, erhält man:
freilegt, erhält man:Der größtmögliche Wert für die Zielvariable ist somit
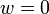 . Das ist derselbe Wert, den auch schon die Anfangslösung hatte, doch war das aus dem ersten Gleichungssystem nicht ersichtlich und ist selbstverständlich nicht immer der Fall.
. Das ist derselbe Wert, den auch schon die Anfangslösung hatte, doch war das aus dem ersten Gleichungssystem nicht ersichtlich und ist selbstverständlich nicht immer der Fall.Besondere Pivotverfahren
Simplexverfahren (auch Primale Simplexverfahren genannt) waren die ersten Pivotverfahren für die Lineare Optimierung und wurden 1947 von George Dantzig veröffentlicht. Diese Pivotverfahren gehen von einer sogenannten zulässigen Basis mit
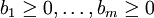 aus und untersuchen ausschließlich zulässige Basen, bis eine Optimalbasis gefunden wird. Eine wichtige Eigenschaft der primalen Simplexverfahren ist, dass der Wert der Zielvariablen, also
aus und untersuchen ausschließlich zulässige Basen, bis eine Optimalbasis gefunden wird. Eine wichtige Eigenschaft der primalen Simplexverfahren ist, dass der Wert der Zielvariablen, also 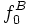 , mit jedem Schritt monoton anwächst; würde er streng monoton anwachsen, wäre die Endlichkeit des Verfahrens gesichert. Ein primales Simplexverfahren muss seine Pivots wie folgt wählen:
, mit jedem Schritt monoton anwächst; würde er streng monoton anwachsen, wäre die Endlichkeit des Verfahrens gesichert. Ein primales Simplexverfahren muss seine Pivots wie folgt wählen:- Wähle ein beliebiges
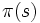 , welches
, welches 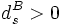 erfüllt. Zum Beispiel (Bland [1]), suche das kleinste
erfüllt. Zum Beispiel (Bland [1]), suche das kleinste 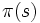 mit dieser Eigenschaft.
mit dieser Eigenschaft. - Wähle ein beliebiges
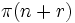 , welches
, welches 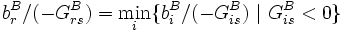 erfüllt. Zum Beispiel (Bland), suche das kleinste
erfüllt. Zum Beispiel (Bland), suche das kleinste 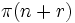 mit dieser Eigenschaft.
mit dieser Eigenschaft.
Um eine zulässige Ausgangsbasis zu erhalten, muss in einer sogenannten 1. Phase eine Hilfsaufgabe gelöst werden.
Ein Standardergebnis der Linearen Optimierung besagt, dass für jede lösbare Aufgabe und für jede zulässige Basis eine Folge zulässiger Pivots existiert, die über ausschließlich zulässige Basen zu einer Optimalbasis führt; unbekannt ist dagegen, ob es eine Folge dieser Art gibt, deren Länge sich polynomial in der Speichergröße der Daten beschränken lässt.
Duale Simplexverfahren sind Pivotverfahren, die von einer sogenannten dual-zulässigen Basis mit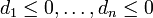 ausgehen, und in ihrer Suche nach einer Optimalbasis ausschließlich dual-zulässige Basen untersuchen; der Wert der Zielvariablen nimmt dabei monoton ab. Duale Simplexverfahren erzeugen die gleichen Pivotfolgen wie die auf die duale Aufgabe angewandten primalen Simplexverfahren, und haben deshalb auch grundsätzlich die gleichen Eigenschaften wie die primalen Verfahren. Dass sie für die Lösung vieler angewandter Aufgaben trotzdem den Primalverfahren vorgezogen werden, liegt daran, dass es für viele angewandte Aufgaben leichter ist, eine gute dual-zulässige Ausgangsbasis zu finden.
ausgehen, und in ihrer Suche nach einer Optimalbasis ausschließlich dual-zulässige Basen untersuchen; der Wert der Zielvariablen nimmt dabei monoton ab. Duale Simplexverfahren erzeugen die gleichen Pivotfolgen wie die auf die duale Aufgabe angewandten primalen Simplexverfahren, und haben deshalb auch grundsätzlich die gleichen Eigenschaften wie die primalen Verfahren. Dass sie für die Lösung vieler angewandter Aufgaben trotzdem den Primalverfahren vorgezogen werden, liegt daran, dass es für viele angewandte Aufgaben leichter ist, eine gute dual-zulässige Ausgangsbasis zu finden.
Criss-Cross-Verfahren (englisch: kreuz und quer) sind allgemeine Pivotverfahren, die von einer beliebigen Basis ausgehen. Ein wichtiger Ansatz bei der Pivotauswahl in den Criss-Cross-Verfahren besteht darin, die Unbekannten in einer mehr oder weniger festen Reihenfolge anzuordnen. Das einfachste aller Criss-Cross-Verfahren verwendet folgende Kleinster-Index-Pivotauswahl[2] (wie üblich, ist das Minimum einer leeren Menge unendlich groß):- Suche
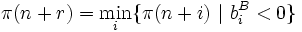 und
und 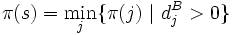 .
. - Falls
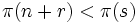 ist, wähle Pivot
ist, wähle Pivot 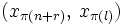 mit
mit 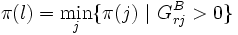 .
. - Falls
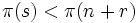 ist, wähle Pivot
ist, wähle Pivot 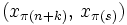 mit
mit 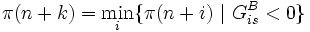 .
.
Die Veränderlichen dürfen beliebig geordnet werden, sollen aber die Anfangsordnung beibehalten.
Während die bekannten Simplexverfahren alle eine überpolynomial beschränkte Laufzeit beanspruchen, sind Laufzeitschranken für die Criss-Cross-Verfahren ein noch (2004) offenes Forschungsthema.[3][4]
Einzelnachweise
- ↑ a b c z. B. in: Vašek Chvátal: Linear Programming. W. H. Freeman and Company, New York, 1983, ISBN 0-716-71587-2
- ↑ a b c Komei Fukuda & Tamás Terlaky (1997): Criss-Cross Methods: A Fresh View on Pivot Algorithms
- ↑ a b Komei Fukuda & Tamás Terlaky (1999): On the Existence of a Short Admissible Pivot Sequences for Feasibility and Linear Optimization Problems
- ↑ Komei Fukuda & Bohdan Kaluzny (2004): The criss-cross method can take Ω(n^d) pivots
Wikimedia Foundation.

![\begin{matrix}
z & = & f_0 & + & d_1\,x_1 & + & \cdots & + & d_n\,x_n
\\[3pt]
x_{n+1} & = & b_1 & + & G_{11}\,x_1 & + & \cdots & + & G_{1n}\,x_n
\\
\vdots & & \vdots & & \vdots & & & & \vdots
\\
x_{n+m} & = & b_m & + & G_{m1}\,x_1 & + & \cdots & + & G_{mn}\,x_n
\end{matrix}](/pictures/dewiki/97/a38ec7c60aa436d8178ef4c4dba4e5fb.png)
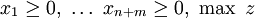
![\begin{matrix}
B=\{x_{\pi(n+1)},\ldots x_{\pi(n+m)}\}
\\[3pt]
\end{matrix}](/pictures/dewiki/101/e2db64a7b5bf7f792e985aab9962d112.png)
![\begin{matrix}
z & = & f^B_0 & + & d^B_1\,x_{\pi(1)} & + & \cdots & + & d^B_n\,x_{\pi(n)}
\\[3pt]
x_{\pi(n+1)} & = & b^B_1 & + & G^B_{11}\,x_{\pi(1)} & + & \cdots & + & G^B_{1n}\,x_{\pi(n)}
\\
\vdots & & \vdots & & \vdots & & & & \vdots
\\
x_{\pi(n+m)} & = & b^B_m & + & G^B_{m1}\,x_{\pi(1)} & + & \cdots & + & G^B_{mn}\,x_{\pi(n)}
\end{matrix}](/pictures/dewiki/98/b2c56d1ffc70b4ad3534054d05407f86.png)
![\begin{matrix}
x_3 & = &( &- ~4 &- ~7x_1 &+ ~2x_2 &)~/~1
\\[2pt]
x_4 & = &( &- ~3 &- ~3x_1 &+ ~~x_2 &)~/~1
\\[2pt]
x_5 & = &( &~~ ~9 &+ ~7x_1 &- ~3x_2 &)~/~1
\end{matrix}](/pictures/dewiki/55/747a750d3279674ec474d8d02cb8a8bb.png)
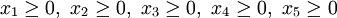
![\begin{matrix}
x_2 & = &( &~~ ~4 &+ ~7x_1 &+ ~~x_3 &)~/~2
\\[2pt]
x_4 & = &( &- ~2 &+ ~~x_1 &+ ~~x_3 &)~/~2
\\[2pt]
x_5 & = &( &~~ ~6 &- ~7x_1 &- ~3x_3 &)~/~2
\end{matrix}](/pictures/dewiki/52/4130064e807a6bcdc7d2306eb9e2bab5.png)
![\begin{matrix}
x_2 & = &( &~~ ~9 &+ ~7x_4 &- ~3x_3 &)~/~1
\\[2pt]
x_1 & = &( &~~ ~2 &+ ~2x_4 &- ~~x_3 &)~/~1
\\[2pt]
x_5 & = &( &- ~4 &- ~7x_4 &+ ~2x_3 &)~/~1
\end{matrix}](/pictures/dewiki/98/b3301c20f264b204eaef6e0f23ac9b33.png)
![\begin{matrix}
x_2 & = &( &~~ ~6 &- ~7x_4 &- ~3x_5 &)~/~2
\\[2pt]
x_1 & = &( &~~ ~0 &- ~3x_4 &- ~~x_5 &)~/~2
\\[2pt]
x_3 & = &( &~~ ~4 &+ ~7x_4 &+ ~~x_5 &)~/~2
\end{matrix}](/pictures/dewiki/100/d6aa724146bf907a8198723994ba71a6.png)
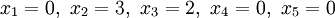
![\begin{matrix}
x_3 & = &(& -~ 3 &-~ 3x_1 &+~ ~x_2 &)~/~1
\\[2pt]
x_4 & = &(& -~ 4 &-~ 7x_1 &+~ \mathbf{2x_2} &)~/~1
\\[2pt]
x_5 & = &(&~~~ 2 &+~ 2x_1 &-~ ~x_2 &)~/~1
\\[2pt]
x_6 & = &(&~~~ 9 &+~ 7x_1 &-~ 3x_2 &)~/~1
\end{matrix}](/pictures/dewiki/101/ee7c2498604a0dde7bee979a4d321c58.png)
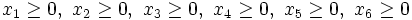
![\begin{matrix}
x_3 & = &(& -~ 2 &+~ ~\mathbf{x_1} &+~ ~x_4 &)~/~2
\\[2pt]
x_2 & = &(&~~~ 4 &+~ 7x_1 &+~ ~x_4 &)~/~2
\\[2pt]
x_5 & = &(&~~~ 0 &-~ 3x_1 &-~ ~x_4 &)~/~2
\\[2pt]
x_6 & = &(&~~~ 6 &-~ 7x_1 &-~ 3x_4 &)~/~2
\end{matrix}](/pictures/dewiki/99/c1e90424aac8aed719e3328a5a22a114.png)
![\begin{matrix}
x_1 & = &(&~~~ 2 &+~ 2x_3 &-~ ~x_4 &)~/~1
\\[2pt]
x_2 & = &(&~~~ 9 &+~ 7x_3 &-~ 3x_4 &)~/~1
\\[2pt]
x_5 & = &(& -~ 3 &-~ 3x_3 &+~ ~x_4 &)~/~1
\\[2pt]
x_6 & = &(& -~ 4 &-~ 7x_3 &+~ \mathbf{2x_4} &)~/~1
\end{matrix}](/pictures/dewiki/54/6b0270835c8c769c045bfb24635458be.png)
![\begin{matrix}
w & = & -f_0 & - & b_1\,y_{n+1} & - & \cdots & - & b_m\,y_{n+m}
\\[3pt]
y_1 & = & -d_1 & - & G_{11}\,y_{n+1} & - & \cdots & - & G_{m1}\,y_{n+m}
\\
\vdots & & \vdots & & \vdots & & & & \vdots
\\
y_n & = & -d_n & - & G_{1n}\,y_{n+1} & - & \cdots & - & G_{mn}\,y_{n+m}
\end{matrix}](/pictures/dewiki/101/ef1d96494755b3d17147f4a0af4444e2.png)
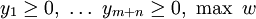
![\begin{matrix}
B=\{y_{\pi(1)},\ldots y_{\pi(n)}\}\subset\{y_1,\ldots y_{n+m}\}
\\[3pt]
\end{matrix}](/pictures/dewiki/57/9be4f604c8e84314a74011bf3f9e9c8c.png)
![\begin{matrix}
w & = & -f^B_0 & - & b^B_1\,y_{\pi(n+1)} & - & \cdots & - & b^B_m\,y_{\pi(n+m)}
\\[3pt]
y_{\pi(1)} & = & -d^B_1 & - & G^B_{11}\,y_{\pi(n+1)} & - & \cdots & - & G^B_{m1}\,y_{\pi(n+m)}
\\
\vdots & & \vdots & & \vdots & & & & \vdots
\\
y_{\pi(n)} & = & -d^B_n & - & G^B_{1n}\,y_{\pi(n+1)} & - & \cdots & - & G^B_{mn}\,y_{\pi(n+m)}
\end{matrix}](/pictures/dewiki/48/07763340c70dbcf8ebb140d83f766d94.png)
![\begin{matrix}
~w~ & = &( & 0 &+ ~4y_3 &+ ~3y_4 &- ~9y_5 &)~/~1
\\[2pt]
y_1 & = &( & 0 &+ ~7y_3 &+ ~3y_4 &- ~7y_5 &)~/~1
\\[2pt]
y_2 & = &( & 0 &- ~2y_3 &- ~~y_4 &+ ~3y_5 &)~/~1
\end{matrix}](/pictures/dewiki/50/270ceb7709edc89d52fc72c65114b71d.png)
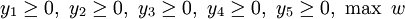
![\begin{matrix}
~w~ & = &( & 0 &- ~4y_2 &+ ~2y_4 &- ~6y_5 &)~/~2
\\[2pt]
y_1 & = &( & 0 &- ~7y_2 &- ~~y_4 &+ ~7y_5 &)~/~2
\\[2pt]
y_3 & = &( & 0 &- ~~y_2 &- ~~y_4 &+ ~3y_5 &)~/~2
\end{matrix}](/pictures/dewiki/102/fffe8ac51e241673fefc96759274220c.png)
![\begin{matrix}
~w~ & = &( & 0 &- ~9y_2 &- ~2y_1 &+ ~4y_5 &)~/~1
\\[2pt]
y_4 & = &( & 0 &- ~7y_2 &- ~2y_1 &+ ~7y_5 &)~/~1
\\[2pt]
y_3 & = &( & 0 &+ ~3y_2 &+ ~~y_1 &- ~2y_5 &)~/~1
\end{matrix}](/pictures/dewiki/48/06a2db947e0e8354eab81210a793f66b.png)
![\begin{matrix}
~w~ & = &( & 0 &- ~6y_2 &+ ~0y_1 &- ~4y_3 &)~/~2
\\[2pt]
y_4 & = &( & 0 &+ ~7y_2 &+ ~3y_1 &- ~7y_3 &)~/~2
\\[2pt]
y_5 & = &( & 0 &+ ~3y_2 &+ ~~y_1 &- ~~y_3 &)~/~2
\end{matrix}](/pictures/dewiki/50/202592e9fa15ef90775f825fbcb8c9b5.png)