Pochhammer-Symbol

Das Pochhammer-Symbol ist eine spezielle Funktion, die in der Kombinatorik und in der Theorie der hypergeometrischen Funktionen verwendet wird. Der Name geht auf Leo August Pochhammer zurück.

Notation

Für das Symbol, das diese Funktion repräsentiert, sind verschiedene Varianten gebräuchlich:

x⁽ⁿ⁾ (u. a. in der Kombinatorik)

(x,n),(x)_n (Analysis, spezielle Funktionen)

(xⁿ) (weitere Varianten)

In der Theorie der speziellen Funktionen wird mit

$(x)_n\,$

die steigende Faktorielle bezeichnet

$(x)_n=x(x+1)(x+2)\cdots(x+n-1)=\frac{(x+n-1)!}{(x-1)!}$,

hingegen wird in der Kombinatorik damit die fallende Faktorielle bezeichnet

$(x)_n=x(x-1)(x-2)\cdots(x-n+1)=\frac{x!}{(x-n)!}$.

Um eine Verwechslung zu vermeiden, wird oftmals (x)ⁿ für die steigenden und (x)_n für die fallenden Faktoriellen verwendet. Des Weiteren gibt es eine neue Notation für die steigenden bzw. fallenden Faktoriellen, die von Ronald L. Graham, Donald E. Knuth und Oren Patashnik in ihren Buch Concrete Mathematics eingeführt wurde.
Für die steigenden Faktoriellen schreiben sie

$x^{\overline{n}}=\frac{(x+n-1)!}{(x-1)!}$,

und für die fallenden Faktoriellen

$x^{\underline{n}}=\frac{x!}{(x-n)!}$.

Die fallenden Fakultäten besitzen in der diskreten Differentialrechnung ähnliche Eigenschaften wie Potenzen bei der Differentialrechnung und können zur Berechnung von Reihen verwendet werden.

Definition im Sinne der speziellen Funktionen

Das Pochhammer-Symbol wird im Allgemeinen über die Gamma-Funktion definiert:

$(x,n) \equiv \frac{\Gamma (x+n)}{\Gamma(x)}$

Für natürliche Zahlen gilt dann

$(m,n) \equiv m (m+1) \dots (m+n-1) ;\quad(m,n \in \mathbb{N})$

Eigenschaften

Graph der ersten vier Pochhammersymbole

• Das Pochhammer-Symbol ist eine meromorphe Funktion
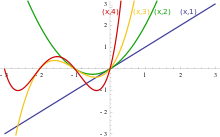
• Ist $n \in \mathbb{N}$, so kann (x,n) als Polynom in x dargestellt werden. Diese haben eine gemeinsame Nullstelle bei x = 0.
• Zusammenhang zwischen Koeffizienten verschiedener Vorzeichen

$(x,-n) = (-1)^n \frac{1}{(1-x,n)}$

• Divisionsregel

$\frac{(x,n)}{(x,m)} = (x+m,n-m) ;\quad n>m$

$\frac{(x,n)}{(x,m)} = (x+n,m-n) ;\quad m>n$

• spezielle Werte

(1,n) = n!

(1 / 2,n) = 2 ^{− n}(2n − 1)!!

(0,0) = 1