- Mathematisches Symbol
-
Die Notation in der mathematischen Symbolschrift erfolgt in der Mathematik (z. B. in Formeln oder Gleichungen) unter der Verwendung von Symbolen. Beispielsweise wird die Addition von zwei Zahlen durch das Zeichen '+' dargestellt. Mehr über die Geschichte der mathematischen Symbolsprache ist im Artikel Mathematische Notation zu finden.
Anmerkungen zum Artikel:
- Die folgenden Tabellen stellen eine Orientierungshilfe dar, weiterführende Informationen zu den einzelnen Symbolen findet man in dem jeweils verlinkten Artikel. Die verschiedenen Bezeichnungen sind nach Teilgebieten der Mathematik unterteilt.
- Außer den Links zu den Fußnoten [1], [2], [3], … sind noch folgende Navigationshilfen verwendet worden:
- [➚] – Link zur Erklärung einer Bezeichnung
Inhaltsverzeichnis
Algebra
Lineare Algebra
Matrizen
Symbol Interpretation Relevante Artikel 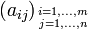
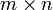 -Matrix
-MatrixMatrix (Mathematik) 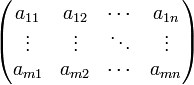
1n  -Einheitsmatrix
-EinheitsmatrixEinheitsmatrix En In diag(d1,d2,...,dn) Diagonalmatrix Diagonalmatrix Matrizenoperationen und -funktionen
Symbol Interpretation Relevante Artikel 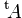
zu A transponierte Matrix Matrix (Mathematik) AT 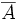
zu A konjugierte Matrix Matrix (Mathematik) 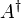
zu A adjungierte Matrix Adjungierte Matrix det(A) Determinante der Matrix A Determinante (Mathematik) | A | adj(A) Adjunkte zu A, zu A komplementäre Matrix Adjunkte 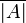
Obere Grenze der quadratischen Matrix A nach Wielandt Grenze einer quadratischen Matrix 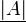
Untere Grenze der quadratischen Matrix A 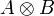
Kronecker-Produkt der Matrizen A und B Kronecker-Produkt Sp(A) Spur der Matrix A Spur (Mathematik) tr(A) χA(λ) charakteristisches Polynom der Matrix A Charakteristisches Polynom rang(A) Rang der Matrix A Rang (Mathematik) rg(A) rk(A) Normen von Matrizen
Symbol Interpretation Relevante Artikel 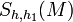
Schrankennorm der Matrix M bezüglich der Vektornormen h und h1 | M | p Höldersche Matrizennorm der Matrix M Moduln und Vektorräume
Symbol Interpretation Relevante Artikel 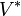
zu dem Vektorraum V duale Vektorraum Dualraum 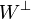
der zu dem Untervektorraum W totalsenkrechte Untervektorraum 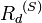
der R-Rechtsmodul der formalen Summen (Linearkombinationen) der nichtleere Menge S über dem Ring R Linearkombination 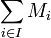 [1]
[1]Summe (äußere direkte Summe) der Moduln (Mi)i Direkte Summe 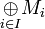 [1]
[1]direkte Summe (innere direkte Summe) der Moduln (Mi)i rg M [1] Rang des Moduls M lA(M) [1] Länge des A-Moduls M Msat [1] Saturierung des Moduls M Körper- und Ringtheorie
Symbol Interpretation Relevante Artikel 
Einheit in einem Ring Einheit 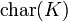
die Charakteristik des Körpers K Charakteristik 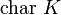 [1]
[1]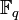
Galoiskörper von q Elementen Endlicher Körper 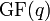 oder
oder 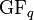
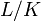
Körpererweiterung (L ist der Oberkörper) Körpererweiterung 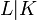
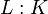
![[L:K]\,](/pictures/dewiki/50/207b9820d8c58bebbde8ecdadfcdd61d.png)
der Grad der Erweiterung L:K Erweiterungsgrad ![[L:K]_{\operatorname{s}}\,](/pictures/dewiki/52/49fce80e48d9121e319430ddee818d2b.png) [1]
[1]Separabilitätsgrad der Erweiterung L:K Separabilität ![[L:K]_{\operatorname{i}}\,](/pictures/dewiki/54/6d4bf9efb68d64a81da536f964ff1fc6.png)
Inseparabilitätsgrad der Erweiterung L:K 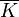 [1]
[1]der algebraische Abschluss des Körpers K Algebraischer Abschluss 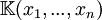 [2]
[2]Körper der rationalen Funktionen mit n Variablen Rationale Funktion 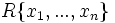
Potenzreihenring über den Ring R[3] Formale Potenzreihe ![R[[x_1,...,x_n]]\,](/pictures/dewiki/99/c26a2b3a07b26b2d980b249ce99d38a9.png)
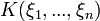
Der kleinste Oberkörper von K, der alle ξ1 bis ξn enthält Einfache Erweiterung 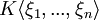
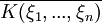 [4]
[4]Algebraische Erweiterung der Quotientenkörper von 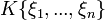 [3]
[3]![K[X_1,...,X_n]\,](/pictures/dewiki/51/3d4458527fbf906fa002e924dc99e4e5.png)
Der kleinste Ring, der den Ring von K als Unterring und alle X1 bis Xn enthält. Polynomring, Polynom (Verallgemeinerung) Elementare Mathematik
Elementare Funktionen
Symbol Interpretation Relevante Artikel 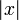
Betrag von x Betragsfunktion 
nimmt den Wert: - − 1 an, falls x < 0
- 0, falls x = 0 und
- 1, falls x > 0
Signum 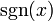
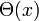
nimmt den Wert 1 an, falls x > 0, sonst: 0 Heaviside-Funktion 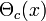
nimmt den Wert c, falls x = 0, sonst: Θ(x) δi,j Kronecker-Delta Kronecker-Delta 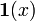
Charakteristische Funktion (auch Indikatorfunktion genannt) Charakteristische Funktion χ(x) Intervalle
Symbol Interpretation Relevante Artikel [a,b] abgeschlossenes (kompaktes) Intervall Intervall 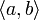
]a,b[ offenes Intervall (a,b) [a,b[ rechts halboffenes Intervall [a,b) 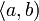
]a,b] links halboffenes Intervall (a,b] 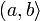
Trigonometrische Funktionen
Symbol Interpretation Relevante Artikel 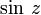
Sinus Sinus und Kosinus 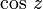
Kosinus 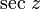
Sekans Sekans und Kosekans 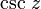
Kosekans 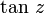
Tangens Tangens und Kotangens 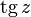
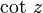
Kotangens 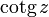
Zyklometrische Funktionen
Symbol Interpretation Relevante Artikel 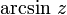
Arkussinus Arkussinus und Arkuskosinus 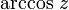
Arkuskosinus 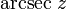
Arkussekans Arkussekans und Arkuskosekans 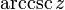
Arkuskosekans 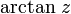
Arkustangens Arkustangens und Arkuskotangens 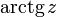
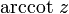
Arkuskotangens 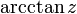
Komplexe Zahlen
Symbol Interpretation Relevante Artikel 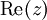
Realteil einer Komplexen Zahl z Komplexe Zahlen – Definition ![\operatorname{Re}[z]](/pictures/dewiki/102/f98397a0b33d7ce4746ebcc75c3914d5.png)
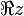
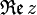
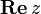
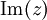
Imaginärteil einer Komplexen Zahl z ![\operatorname{Im}[z]](/pictures/dewiki/49/143594d709d5cfb541ba809a1e3b1728.png)
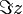
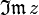
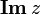
i Imaginäre Einheit i mit i2 = − 1 Komplexe Zahlen j Imaginäre Einheit j mit j2 = − 1 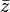
Die konjugiert komplexe Zahl zu z Konjugation (Mathematik) z * Geometrie
Elementargeometrie
Symbol Interpretation Relevante Artikel 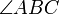
Winkel mit Schenkeln BA und BC Winkel 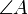
Winkel mit Scheitelpunkt A 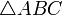
Dreieck mit Eckpunkten A, B und C Dreieck 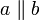
die Geraden a und b sind parallel zueinander Parallel (Geometrie) 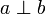
die Geraden a und b sind orthogonal zueinander Orthogonalität Differentialgeometrie
Vektorrechnung
Symbol Interpretation Relevante Artikel 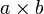
Kreuzprodukt (Vektorprodukt, äußeres Produkt, vektorielles Produkt) der Vektoren a und b Kreuzprodukt [a,b] 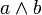
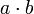
Inneres Produkt (Skalarprodukt, Punktprodukt) der Vektoren a und b Skalarprodukt (a,b) ab 
Nablavektor Nabla-Operator 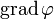
Gradient vom differenzierbaren Skalarfeldes 
Gradient (Mathematik) 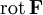
vektorielle Rotation vom dreidimensionalen differenzierbaren Vektorfeld 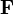
Rotation (Mathematik) 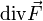
Divergenz des Vektorfeldes 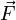
Divergenz (Mathematik) Δ elliptischer Differentialoperator Laplace-Operator 
hyperbolischer Differentialoperator D’Alembert-Operator Mengenlehre
Mengentheoretische Funktionen
Symbol Interpretation Relevante Artikel 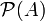
Potenzmenge (die Menge aller Untermengen) einer Menge A Potenzmenge 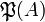
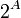
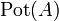
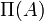
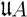
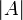
Mächtigkeit (Kardinalität) einer Menge A Mächtigkeit (Mathematik) 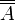
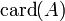
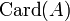
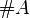
Kardinalzahlen
Symbol Interpretation Relevante Artikel 
die Mächtigkeit von  [5]
[5]Kardinalzahl 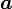
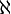 [6]
[6]die Mächtigkeit von 
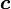 [7]
[7]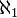
die kleinste Kardinalzahl größer als 
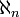
die kleinste Kardinalzahl größer als 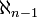
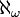
die kleinste Kardinalzahl größer als alle 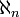
Mengenoperationen
Symbol Interpretation Relevante Artikel 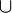
Vereinigung von zwei Mengen, z. B.: 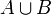 bzw.
bzw. 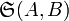
oder von Elementen einer Mengenfamilie, z. B.:
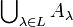 bzw.
bzw. 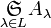 ;
;manchmal wird auch die Bezeichnung A + B verwendet, allerdings wird dann auch vorausgesetzt, dass A und B disjunkt sind[6]
Vereinigungsmenge 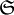 [6]
[6]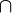
Durchschnitt von Mengen z. B.: 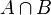 [8] bzw.
[8] bzw. 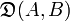 oder:
oder: 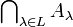 bzw.
bzw. 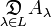
Schnittmenge 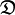 [6]
[6]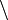
Differenz z. B.: 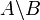 .
.
Manchmal wird auch die Bezeichnung A − B verwendet, allerdings wird dann oft vorausgesetzt, dass
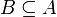
Differenz und Komplement 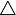
symmetrische Differenz z. B.: 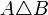
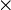
kartesisches Produkt z. B.: 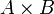 für das kartesische Produkt von zwei Mengen und
für das kartesische Produkt von zwei Mengen und
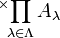 oder
oder 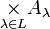 für das kartesische Produkt einer Mengenfamilie
für das kartesische Produkt einer MengenfamilieKartesisches Produkt 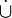
disjunkte Vereinigung Disjunkte Vereinigung 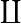
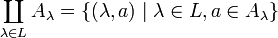
Mengenrelationen
Symbol Interpretation Relevante Artikel 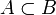
A ist echte Teilmenge von B Teilmenge 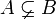
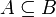
A ist Teilmenge von B 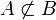
A ist keine Teilmenge von B 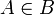
A ist Element von B Menge (Mathematik) 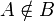
A ist kein Element von B 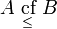
die gerichtete oder halbgeordnete Menge (Klasse) (A, 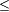 ) ist mit ihrer Teilmenge (Teilklasse) B konfinal
) ist mit ihrer Teilmenge (Teilklasse) B konfinal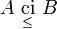
die gerichtete oder halbgeordnete Menge (Klasse) (A, 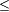 ) ist mit ihrer Teilmenge (Teilklasse) B koinitial
) ist mit ihrer Teilmenge (Teilklasse) B koinitialOrdinalzahlen und Ordnungstypen
Symbol Interpretation Relevante Artikel 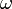
der Ordnungstyp (die Ordinalzahl) von  ,[5]
,[5]Ordinalzahl 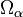
die kleinste Ordinalzahl, die den Ordnungstyp einer Menge mit Mächtigkeit 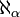 darstellt[5]
darstellt[5]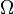
die kleinste Ordinalzahl, die den Ordnungstyp einer Menge mit Mächtigkeit 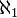 darstellt[5]
darstellt[5]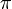
der Ordnungstyp von  ,[5]
,[5]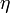
der Ordnungstyp von  ,[5]
,[5]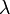
der Ordnungstyp von  ,[5]
,[5]
die kleinste Ordinalzahl größer als alle 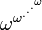 [5]
[5]Spezielle Funktionen
Fehlerfunktionen
Symbol Interpretation Relevante Artikel erf(z) Fehlerfunktion von z Fehlerfunktion erfc(z) komplementäre Fehlerfunktion von z erfi(z) imaginäre Fehlerfunktion von z Zahlentheorie
Zahlenmengen
Symbol Interpretation Relevante Artikel 
die Menge der natürlichen Zahlen Natürliche Zahl 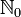
die Menge der natürlichen Zahlen einschließlich der Null 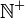
die Menge der natürlichen Zahlen ohne die Null 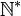
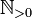
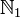

die Menge der ganzen Zahlen Ganze Zahl 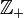
die Menge der positiven ganzen Zahlen 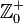
die Menge der positiven ganzen Zahlen und der Null 
die Menge der rationalen Zahlen Rationale Zahl 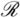 [7]
[7]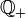
die Menge der positiven rationalen Zahlen (manchmal wird mit
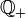 die Menge der nicht negativen und mit
die Menge der nicht negativen und mit 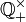 die Menge der positiven rationalen Zahlen bezeichnet[9])
die Menge der positiven rationalen Zahlen bezeichnet[9])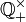
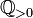 [1]
[1]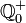
die Menge der positiven rationalen Zahlen und der Null 
die Menge der reellen Zahlen Reelle Zahl 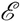 [7]
[7]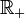
die Menge der positiven reellen Zahlen (oder
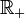 die Menge der nicht negativen und
die Menge der nicht negativen und 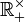 die Menge der positiven reellen Zahlen[9])
die Menge der positiven reellen Zahlen[9])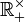
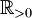 [1]
[1]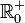
die Menge der positiven reellen Zahlen und der Null 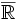
die Menge der erweiterten reellen Zahlen Reelle Zahl 
die Menge der komplexen Zahlen Komplexe Zahl 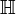
die Menge der Quaternionen Hyperkomplexe Zahl 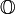
die Menge der Oktonionen 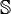
die Menge der Sedenionen Teilbarkeit
Symbol Interpretation Relevante Artikel 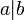
a teilt b Teilbarkeit 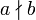
a teilt b nicht 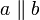
a ist eigentlicher (nichttrivialer) Teiler von b (a ist also ungleich 1, − 1, − b oder b)[3] 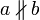
a ist kein eigentlicher Teiler von b 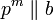
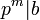 und
und 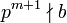 [10]
[10]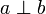
a und b sind teilerfremd Teilerfremdheit 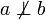
a und b sind nicht teilerfremd Elementare arithmetische Funktionen
Symbol Interpretation Relevante Artikel 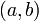
größter gemeinsamer Teiler von a und b Größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches  [11]
[11]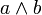
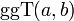
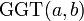
![[a,b]\,\!](/pictures/dewiki/56/8b596d04e319e05cadcc7dcf251a9815.png)
kleinstes gemeinsames Vielfaches von a und b  [11]
[11]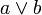
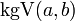
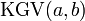
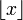
Ganzzahl-Funktion Gaußklammer ![[ x ]\,](/pictures/dewiki/52/4a22212722affbc9a91e41a18af45fc0.png)
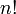
Fakultät von n Fakultät 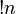
Subfakultät von n Subfakultät 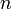 ¡[12]
¡[12]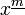 [12]
[12]Fallende Faktorielle Fallende Faktorielle, Pochhammer-Symbol 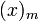
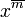 [12]
[12]Steigende Faktorielle Fallende Faktorielle, Pochhammer-Symbol 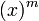
![[a=b]\,](/pictures/dewiki/51/3286df33babebeb3c70ab48f9ad7fc1e.png)
nimmt den Wert 1, wenn a = b, sonst 0[12] ![[a\bot b]\,](/pictures/dewiki/52/47d822a0b4f6509c5b9c4c85d36ace5e.png)
nimmt den Wert 1, wenn a und b teilerfremd sind, sonst 0[12] Multiplikative zahlentheoretische Funktionen
Symbol Interpretation Relevante Artikel 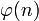
Anzahl der primen Restklassen Modulo n Eulersche φ-Funktion 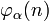
Jordansche Funktion[13],[14] Jordansche Funktion 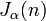
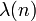
Liouvillesche Funktion[15] 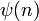
Dedekindsche ψ-Funktion Dedekindsche Psi-Funktion 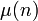
Möbiusfunktion Möbiusfunktion 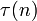
Ramanujansche tau-Funktion S. A. Ramanujan - Ramanujansche Tau-Funktion Anzahl der Teiler von n Teileranzahlfunktion 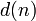
Anzahl der Teiler von n Teileranzahlfunktion 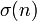
Summe der Teiler von n Teilersumme 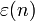
1 für n = 1 und 0 sonst (Einheitselement in der Gruppe der multiplikativen zahlentheoretischen Funktionen) Faltung 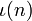
das inverse Element von μ(n) (1 für alle n)[16] Dirichletreihe der Möbiusfunktion, Faltung 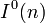
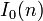
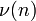
Identität (n für alle n) 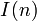
Weitere Funktionen aus der analytischen Zahlentheorie
Symbol Interpretation Relevante Artikel 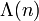
Mangoldt-Funktion Dirichletreihe der Λ-Funktion 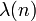
Carmichael-Funktion Carmichael-Funktion 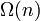
die Anzahl der (nicht unbedingt unterschiedlichen) Primfaktoren von n Primfaktorzerlegung 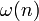
die Anzahl der unterschiedlichen Primfaktoren von n 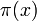
die Anzahl der Primzahlen kleiner gleich x Verteilung der Primzahlen, Primzahlsatz 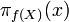
die Anzahl der natürlichen Zahlen n kleiner gleich x, für die | f(n) | eine Primzahl ist 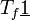
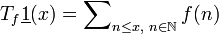 [16]
[16]Atle Selberg, Primzahlsatz 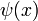
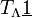 [10],[16],[17],[18]
[10],[16],[17],[18]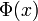
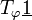 ,[17]
,[17]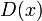
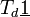 ,[19],[17]
,[19],[17]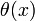
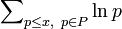
wobei P die Menge der Primzahlen ist (Tschebyscheffsche Funktion)[14],[17]
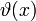
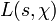
Dirichletsche L-Reihe Dirichletsche L-Reihe Siehe auch
Einzelnachweise und Anmerkungen
- ↑ a b c d e f g h i j S. Bosch: Algebra. Springer, 2004, ISBN 3-540-40388-4.
- ↑ W. Koepf: Computeralgebra – Eine algorithmisch orientierte Einführung. Springer, 2006, ISBN 978-3-540-29894-6.
- ↑ a b c J. Naas, H. L. Schmid: Mathematisches Wörterbuch. B. G. Teubner, Stuttgart 1979, ISBN 3-519-02400-4
- ↑ C. Chevalley: Introduction to the theory of algebraic functions of one variable. American Mathematical Society, New York 1951.
- ↑ a b c d e f g h I. P. Natanson: Theorie der Funktionen einer reellen Veränderlichen. Verlag Harri Deutsch, Frankfurt am Main 1977, ISBN 3-87144-217-8. (auch in digitaler Form auf russisch bei INSTITUTE OF COMPUTATIONAL MODELLING SB RAS, Krasnojarsk)
- ↑ a b c d F. Hausdorff: Grundzüge der Mengenlehre. Chelsea Publishing Company, New York 1949 (1914).
- ↑ a b c K. Kuratowski: Introduction to Set Theory and Topology. Polish Scientific Publishers, Warszawa 1961.
- ↑ Etwas ältere Bezeichnung ist AB.
- ↑ a b A. Leutbecher: Zahlentheorie. Springer, 1996, ISBN 3-540-58791-8.
- ↑ a b P. Ribenboim: The New Book of Prime Number Records. Springer, 1996, ISBN 0-387-94457-5.
- ↑ a b H. Siemon: Einführung in die Zahlentheorie. Verlag Dr. Kovac, Hamburg 2002, ISSN 1435-6511.
- ↑ a b c d e R. Graham, D. Knuth, O. Patashnik: Concrete Mathematics: A Foundation for Computer Science. Addison-Wesley, 1994, ISBN 0-201-55802-5.
- ↑ J. Schulte: Über die Jordansche Verallgemeinerung der Eulerschen Funktion. uni-siegen.de (pdf)
- ↑ a b J. Sándor, D. Mitrinovic, B. Crstici: Handbook of Number Theory I. Springer, 2005, ISBN 1402042159.
- ↑ Liouville function, en.wikipedia.org
- ↑ a b c H. Scheid: Zahlentheorie. BI-Wiss.-Verl., 1991, ISBN 3-411-14841-1.
- ↑ a b c d K. Chandrasekaran: Introduction to analytic number theory. Springer, 1968.
- ↑ Auch als Tschebyscheffsche Funktion bekannt.
- ↑ Divisor summatory function, en.wikipedia.org
Wikimedia Foundation.
