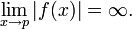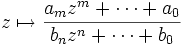- Meromorph
-
Für viele Fragestellungen der Funktionentheorie ist der Begriff der holomorphen Funktion zu speziell. Dies liegt daran, dass der Kehrwert
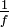 einer holomorphen Funktion f an einer Nullstelle von f eine Definitionslücke hat und somit
einer holomorphen Funktion f an einer Nullstelle von f eine Definitionslücke hat und somit 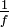 dort auch nicht holomorph ist. Man führt daher den allgemeineren Begriff der meromorphen Funktion ein, die auch isolierte Polstellen besitzen kann.
dort auch nicht holomorph ist. Man führt daher den allgemeineren Begriff der meromorphen Funktion ein, die auch isolierte Polstellen besitzen kann.Meromorphe Funktionen lassen sich lokal als Laurentreihen mit abbrechendem Hauptteil darstellen. Ist U ein Gebiet von
 , so bildet die Menge der auf U meromorphen Funktionen einen Körper.
, so bildet die Menge der auf U meromorphen Funktionen einen Körper.Inhaltsverzeichnis
Definition
Auf dem Körper der komplexen Zahlen
Es sei D eine nichtleere offene Teilmenge der Menge
 der komplexen Zahlen und Pf eine weitere Teilmenge von
der komplexen Zahlen und Pf eine weitere Teilmenge von  , die nur aus isolierten Punkten besteht. Eine Funktion f heißt meromorph, wenn sie für Werte aus
, die nur aus isolierten Punkten besteht. Eine Funktion f heißt meromorph, wenn sie für Werte aus 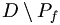 definiert und holomorph ist und für Werte aus Pf Pole hat. Pf wird als Polstellenmenge von f bezeichnet.
definiert und holomorph ist und für Werte aus Pf Pole hat. Pf wird als Polstellenmenge von f bezeichnet.Auf einer riemannschen Fläche[1]
Sei X eine riemannsche Fläche und Y eine offene Teilmenge von X. Unter einer meromorphen Funktion auf Y verstehen wir eine holomorphe Funktion
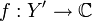 , wobei
, wobei 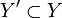 eine offene Teilmenge ist, so dass die folgenden Eigenschaften gelten:
eine offene Teilmenge ist, so dass die folgenden Eigenschaften gelten:- Die Menge
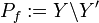 hat nur isolierte Punkte.
hat nur isolierte Punkte. - Für jeden Punkt
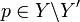 gilt
gilt
Die Punkte aus der Menge
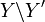 werden Pole von f genannt. Die Menge aller meromorphen Funktionen auf Y wird mit
werden Pole von f genannt. Die Menge aller meromorphen Funktionen auf Y wird mit 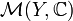 bezeichnet und bildet, falls Y zusammenhängend ist, einen Körper. Dies Definition ist natürlich äquivalent zur Definition auf den Komplexen Zahlen, falls X eine Teilmenge derer ist.
bezeichnet und bildet, falls Y zusammenhängend ist, einen Körper. Dies Definition ist natürlich äquivalent zur Definition auf den Komplexen Zahlen, falls X eine Teilmenge derer ist.Beispiele
- Alle holomorphen Funktionen sind auch meromorph, da ihre Polstellenmenge jeweils leer ist.
- Die Kehrwertfunktion
 ist meromorph; ihre Polstellenmenge ist {0}. Allgemeiner sind alle rationalen Funktionen
ist meromorph; ihre Polstellenmenge ist {0}. Allgemeiner sind alle rationalen Funktionen
- meromorph. Die Polstellenmenge ist hier jeweils eine Teilmenge der Nullstellenmenge des Nennerpolynoms.
- Für jede meromorphe Funktion
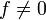 ist ihr Kehrwert
ist ihr Kehrwert 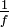 ebenfalls meromorph.
ebenfalls meromorph.
- Die Funktion
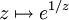 ist nicht auf ganz
ist nicht auf ganz  (und auf keiner Umgebung von 0) meromorph, da 0 keine Polstelle, sondern eine wesentliche Singularität dieser Funktion ist.
(und auf keiner Umgebung von 0) meromorph, da 0 keine Polstelle, sondern eine wesentliche Singularität dieser Funktion ist.
Einzelnachweis
- ↑ Otto Forster - Lectures on Riemann Surfaces (Springer Verlag, 1981)
- Die Menge
Wikimedia Foundation.