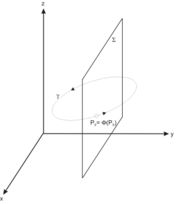
Poincaré-Abbildung — Illustration der Wiederkehr einer Trajektorie nach S. Die Poincaré Abbildung (auch Poincaré map, first return map, nach dem französischen Mathematiker Henri Poincaré) ist eine mathematische Methode zur Untersuchung des Flusses eines… … Deutsch Wikipedia
Henri Poincare — Henri Poincaré Jules Henri Poincaré [pwɛ̃kaˈʀe] (* 29. April 1854 in Nancy; † 17. Juli 1912 in Paris) war ein bedeutender französischer Mathematiker, theoretischer Physiker und Philosoph. Seine Forschungen hatten auch starke Wi … Deutsch Wikipedia
Jules Henri Poincaré — Henri Poincaré Jules Henri Poincaré [pwɛ̃kaˈʀe] (* 29. April 1854 in Nancy; † 17. Juli 1912 in Paris) war ein bedeutender französischer Mathematiker, theoretischer Physiker und Philosoph. Seine Forschungen hatten auch starke Wi … Deutsch Wikipedia
Henri Poincaré — Henri Poincarés Unterschrift Jules Henri Poincaré [ … Deutsch Wikipedia
Siebformel von Poincaré-Sylvester — Das Prinzip von Inklusion und Exklusion (auch Prinzip der Einschließung und Ausschließung oder Einschluss/Ausschluss Verfahren) ist eine hilfreiche Technik zur Bestimmung der Mächtigkeit einer Menge. Sie findet vor allem in der Kombinatorik und… … Deutsch Wikipedia
Siebformel von Poincaré und Sylvester — Das Prinzip von Inklusion und Exklusion (auch Prinzip der Einschließung und Ausschließung oder Einschluss/Ausschluss Verfahren) ist eine hilfreiche Technik zur Bestimmung der Mächtigkeit einer Menge. Sie findet vor allem in der Kombinatorik und… … Deutsch Wikipedia
Van-der-Pol-System — Der Van der Pol Oszillator ist ein schwingungsfähiges System mit nichtlinearer Dämpfung und Selbsterregung. Für kleine Amplituden ist die Dämpfung negativ (die Amplitude wird vergrößert). Ab einem bestimmten Schwellwert der Amplitude wird die… … Deutsch Wikipedia
Bifurkation (Mathematik) — Eine Bifurkation oder Verzweigung ist eine qualitative Zustandsänderung in nichtlinearen Systemen unter Einfluss eines Parameters μ. Der Begriff der Bifurkation wurde von Henri Poincaré eingeführt. Nichtlineare Systeme, deren Verhalten von einem… … Deutsch Wikipedia
Chaos-Theorie — Die Chaosforschung (auch: Theorie komplexer Systeme oder Komplexitätstheorie) ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den… … Deutsch Wikipedia
Chaos Theorie — Die Chaosforschung (auch: Theorie komplexer Systeme oder Komplexitätstheorie) ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den… … Deutsch Wikipedia