- Poincaré-Abbildung
-
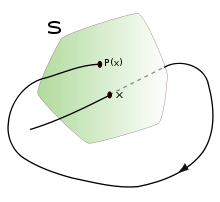
Die Poincaré-Abbildung (auch Poincaré map, first return map, nach dem französischen Mathematiker Henri Poincaré) ist eine mathematische Methode zur Untersuchung des Flusses eines kontinuierlichen n-dimensionalen dynamischen Systems. Dazu betrachtet man die Schnittpunkte einer Trajektorie mit einer (n-1)-dimensionalen transversalen Hyperfläche Σ, dem Poincaré-Schnitt. Die Poincaré-Abbildung ist die Abbildung die jedem dieser Schnittpunkte x den jeweils nächsten P(x) zuordnet und ist somit ein (n-1)-dimensionales diskretes dynamischen Systems.
Inhaltsverzeichnis
Beispiel
Betrachte die Differentialgleichung
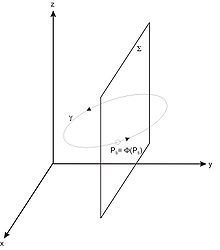
 und bezeichne mit Φ(t,x) den Fluss, also die Lösung zur Anfangsbedingung Φ(0,x) = x. Angenommen es gibt eine periodische Trajektorie, also eine Lösung Φ(t,p) die bei p startet und nach einer bestimmten Zeit τ wieder dorthin zurückkehrt, Φ(τ,p) = p. Dann kann man eine Fläche Σ die transversal zur Trajektorie Φ(t,p) ist und diese in p schneidet wählen. Alle Punkte
und bezeichne mit Φ(t,x) den Fluss, also die Lösung zur Anfangsbedingung Φ(0,x) = x. Angenommen es gibt eine periodische Trajektorie, also eine Lösung Φ(t,p) die bei p startet und nach einer bestimmten Zeit τ wieder dorthin zurückkehrt, Φ(τ,p) = p. Dann kann man eine Fläche Σ die transversal zur Trajektorie Φ(t,p) ist und diese in p schneidet wählen. Alle Punkte  die in der Nähe von p starten werden dann nach einer bestimmten Zeit wieder die Fläche schneiden. Es gibt also eine kleinste positive Zeit τ(x) für die
die in der Nähe von p starten werden dann nach einer bestimmten Zeit wieder die Fläche schneiden. Es gibt also eine kleinste positive Zeit τ(x) für die  gilt. Dann ist die Poincaré-Abbildung gegeben durch P(x) = Φ(τ(x),x). Speziell für die periodische Trajektorie erhält man einen Fixpunkt: P(p) = p. Die Frage ob die periodische Trajektorie stabil ist, ist nun äquivalent zur Frage ob der entsprechende Fixpunkt der Poincaré-Abbildung stabil ist.
gilt. Dann ist die Poincaré-Abbildung gegeben durch P(x) = Φ(τ(x),x). Speziell für die periodische Trajektorie erhält man einen Fixpunkt: P(p) = p. Die Frage ob die periodische Trajektorie stabil ist, ist nun äquivalent zur Frage ob der entsprechende Fixpunkt der Poincaré-Abbildung stabil ist.Anwendung
Die Poincaré-Abbildung ist besonders zur Untersuchung der geometrischen Strukturen chaotischer Attraktoren geeignet, da die zeitliche Diskretisierung eine wesentliche Vereinfachung darstellt.[1]
Literatur
- Herbert Amann: Gewöhnliche Differentialgleichungen. 2 Auflage. de Gruyter, Berlin 1995, ISBN 3-11-014582-0.
- D. V. Anosov: Poincaré return map. In: Michiel Hazewinkel (Hrsg.): Encyclopaedia of Mathematics. Springer-Verlag, Berlin 2002, ISBN 1-4020-0609-8.
- Gerald Teschl: Ordinary Differential Equations and Dynamical Systems. American Mathematical Society, Providence 2011 (freie Onlineversion).
Einzelnachweise
- ↑ Manfred von Ardenne et. al.: Effekte der Physik und ihre Anwendungen. Verlag Harry Deutsch, Frankfurt 2005. ISBN 3-8171-1682-9 S. 1130
Wikimedia Foundation.