Potenzform

Als wissenschaftliche Notation (englisch: scientific notation) bezeichnet man die beiden Varianten moderner Zahlendarstellung:
die Exponentialdarstellung, auch traditionelle wissenschaftliche Notation oder Normdarstellung genannt, und die sogenannte technische Notation (englisch: engineering notation).

• Die traditionelle wissenschaftliche Notation, die immer nur eine – von Null verschiedene – linksseitige Dezimalstelle duldet, wird im Artikel Exponentialdarstellung behandelt. Der Vorteil ist in der Wissenschaft der schnelle Überblick über die Größenordnung und der evtl. Vergleich mehrerer Zahlenwerte. Normalerweise wird eine Zahl in folgendem Format angegeben: 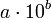$a\cdot10^b$ Der Nachteil dieses Notationsformats ist, dass in der Praxis die Ergebnisse meist „nachformatiert“ werden, um sie mit SI-Symboleinheiten verwenden bzw. sie als Zahlen im Zillionensystem ausdrücken zu können.

• In der technischen Notation werden als Exponenten ausschließlich ganzzahlige Vielfache von 3 verwendet, also ganzzahlige Potenzen von Tausend, eben weil diese den genormten Größenordnungen mikro, milli, kilo, Mega und so weiter entsprechen (siehe Tabelle weiter unten.)

Wissenschaftliche Taschenrechner

Die meisten modernen Taschenrechner können Zahlen automatisch in wissenschaftlicher Notation darstellen (Anzeige im Display: SCI). Bei sehr großen Zahlen oder sehr kleinen Dezimalbrüchen ist dies meist ohnehin nicht anders möglich.

Der Begriff wissenschaftliche Notation wird allerdings nicht ganz einheitlich verwendet, sondern sehr oft auch einfach – besonders im Englischen – synonym zur traditionellen wissenschaftlichen Notation – also zur Exponentialdarstellung – benutzt. Auf Taschenrechnern wird die hier besprochene Variante meist mit ENG (engineering notation) bezeichnet.

Wenn keine hochgestellten Ziffern zur Verfügung stehen, wird die folgende Schreibweise genutzt: aus 10¹⁸ wird 1 E18. Die Zahl 3200 z. B. kann somit auch 3,200 E3 notiert werden. (Siehe auch Exponentialdarstellung)

Präzision im SI- und ENG-Format

Manchmal wurde sowohl den SI-Größenordnungen als auch dem Ingenieurformat vorgeworfen, Zweifel an der Präzision der ermittelten Werte aufkommen zu lassen.

In der Tat gibt die Exponentialdarstellung auf sehr einfache und klare Weise die Präzision der Ergebnisse wieder; nämlich durch die Anzahl der nachstelligen Ziffern. Beispielsweise bedeuten die folgenden Ergebnissen: 5 E-4 m, 5,0 E-4 m und 5,00 E-4 m eben nicht das Gleiche. Diese drei verschiedenen Ergebnisse müssten aber sowohl im SI- als auch im ENG-Format unterschiedslos auf 500 µm bzw. 500 E-6 m reduziert werden.

Nun sind auf nicht mehr als zwei Dezimalstellen ermittelbare Ergebnisse in der Wissenschaft ohnehin eher selten. Dennoch gibt es auch einen „schlauen Kniff“, wie dieses scheinbare Manko des SI- und ENG-Formates aufgehoben werden kann. Die Ergebnisse werden einfach als Dezimalbrüche der übergeordneten Größenordnung angegeben. Im obigen Beispiel jeweils als 0,5 mm, 0,50 mm und 0,500 mm bzw. als 0,5 E-3 m, 0,50 E-3 m und 0,500 E-3 m. Die Angabe der Präzision ist wieder hergestellt.

Die auf drei Stellen genau bestimmte Lichtgeschwindigkeit von 0,300 Gm/s könnte ebenso problemlos dargestellt werden; dies auch, wenn es bekanntlich die Geschwindigkeit von einem Gm/s gar nicht gibt. Gleichwohl aber kann die Lichtgeschwindigkeit seit 1983 ohnehin nicht mehr gemessen werden. Es handelt sich hierbei um einen definierten Wert, von dem jetzt umgekehrt das Längenmaß Meter abgeleitet wird.

Größenordnungen der technischen Notation

10N	Symbol	Name	Dezimalzahl	1000N	Zahlwort
1024	Y	Yotta	1 000 000 000 000 000 000 000 000	10008	Quadrillion
1021	Z	Zetta	1 000 000 000 000 000 000 000	10007	Trilliarde
1018	E	Exa	1 000 000 000 000 000 000	10006	Trillion
1015	P	Peta	1 000 000 000 000 000	10005	Billiarde
1012	T	Tera	1 000 000 000 000	10004	Billion
109	G	Giga	1 000 000 000	10003	Milliarde
106	M	Mega	1 000 000	10002	Million
103	k	Kilo	1 000	10001	Tausend
100	–	Einheit	1	10000	Eins
10−3	m	Milli	0,001	1000−1	Tausendstel
10−6	µ	Mikro	0,000 001	1000−2	Millionstel
10−9	n	Nano	0,000 000 001	1000−3	Milliardstel
10−12	p	Pico	0,000 000 000 001	1000−4	Billionstel
10−15	f	Femto	0,000 000 000 000 001	1000−5	Billiardstel
10−18	a	Atto	0,000 000 000 000 000 001	1000−6	Trillionstel
10−21	z	Zepto	0,000 000 000 000 000 000 001	1000−7	Trilliardstel
10−24	y	Yokto	0,000 000 000 000 000 000 000 001	1000−8	Quadrillionstel

Siehe auch

• Vorsätze für Maßeinheiten