Programmiersprache Haskell

Haskell
Basisdaten
Paradigmen:	funktional, nicht-strikt, modular
Erscheinungsjahr:	1990
Entwickler:	Simon Peyton-Jones, Paul Hudak[1], Philip Wadler, et.al.
Aktuelle Version:	Haskell 98, Haskell Prime in Arbeit  (1998)
Typisierung:	statisch, stark, Typabgleich
wichtige Implementierungen:	GHC, Hugs, NHC, JHC, Yhc
Dialekte:	Helium, Gofer
Einflüsse:	APL, LISP, Miranda, ML
Beeinflusste:	Scala, Cayenne, Clean
haskell.org

Haskell ist eine rein funktionale Programmiersprache, benannt nach dem US-amerikanischen Mathematiker Haskell Brooks Curry, dessen Arbeiten zur mathematischen Logik eine Grundlage funktionaler Programmiersprachen bilden. Haskell basiert auf dem Lambda-Kalkül, weshalb auch der griechische Buchstabe Lambda als Logo verwendet wird. Die wichtigsten Implementierungen sind der Glasgow Haskell Compiler (GHC) und Hugs, ein Haskell-Interpreter.

Entwicklung

Gegen Ende der 1980er Jahre gab es bereits einige funktionale Programmiersprachen. Um der Wissenschaft eine einheitliche Forschungs- und Entwicklungsbasis bereitzustellen, sollte eine standardisierte und moderne Sprache die funktionale Programmierung vereinheitlichen. Zunächst wollte man dazu Miranda als Ausgangspunkt benutzen; doch deren Entwickler waren daran nicht interessiert. So wurde 1990 Haskell 1.0 veröffentlicht.

Die aktuelle Version der Programmiersprache ist eine überarbeitete Variante des Haskell-98-Standards von 1999. Haskell ist die funktionale Sprache, an der zurzeit am meisten geforscht wird. Demzufolge sind die Sprachderivate zahlreich; dazu zählen Parallel Haskell, Distributed Haskell (ehemals Goffin), Eager Haskell, Eden mit einem neuen Ansatz zum parallelen Programmieren und Bedarfsauswertung, DNA-Haskell und sogar objektorientierte Varianten (Haskell++, O'Haskell, Mondrian). Des Weiteren diente Haskell beim Entwurf neuer Programmiersprachen als Vorlage. So wurde z.B. im Falle von Python die Lambda-Notation sowie Listenverarbeitungssyntax übernommen.

Eigenschaften

Programmfluss

• Haskell ist eine rein funktionale Programmiersprache. Funktionen geben nur Werte zurück, ändern aber nicht den Zustand eines Programms (d.h. Funktionen haben keine Seiteneffekte). Das Ergebnis einer Funktion hängt deshalb nur von den Eingangsparametern ab, und nicht, wann oder wie oft die Funktion aufgerufen wird. (s. funktionale Programmierung)

• Es gibt keine imperativen Sprachkonstrukte. Durch Monaden ist es möglich, Ein- und Ausgabeoperationen und zustandsabhängige Berechnungen wie Zufallsgeneratoren rein funktional zu behandeln.

• Es gibt keine Operationen, die einen Variablenwert verändern. So gibt es auch keine Unterscheidung zwischen Variablen und Konstanten und man braucht keine const-Attribute wie in C.

• Zwischen Identität und Gleichwertigkeit von Objekten wird nicht unterschieden.

• Da Seiteneffekte fehlen, sind Programmbeweise beträchtlich einfacher.

• Haskell ist nicht-strikt. Es werden nur Ausdrücke ausgewertet, die für die Berechnung des Ergebnisses gebraucht werden.

 first x y = x
 quadrat x = x * x

Die Funktion first liefert bei Eingabe zweier Parameter den ersten als Ergebnis zurück. Bei der Eingabe von first x (3+7) ist die Auswertung der Summe (3+7) zur Ergebnisbestimmung nicht notwendig, sollte also unberücksichtigt bleiben.

Die Funktion quadrat berechnet bei Eingabe eines Parameters dessen Quadrat. Bei Eingabe von quadrat(3+5), was im Laufe des Auswertungsprozesses zu (3+5)*(3+5) wird, wäre eine doppelte Berechnung der Summe (3+5) ineffizient, sollte also vermieden werden.

Die Auswertungsstrategie, welche die beiden eben geschilderten Probleme umgeht, wird Bedarfsauswertung (engl. lazy evaluation) genannt und kommt in Haskell meist zum Einsatz.

Die Bedarfsauswertung ist vor allem wegen der strengen Einhaltung des funktionalen Konzepts möglich. Umgekehrt macht die Bedarfsauswertung die funktionale Programmierung angenehmer, denn sie erlaubt es besser, Funktionen zur reinen Berechnung von Ein-/Ausgabefunktionen zu trennen.

Die Bedarfsauswertung erlaubt das Arbeiten mit undefinierten Werten und potentiell unendlich großen Datenmengen. So kann man elegant mit Potenzreihen, Zeitreihen (etwa Audiosignalströmen), Kettenbruchzerlegungen, Entscheidungsbäumen und ähnlichem umgehen. Aber auch bei endlichen, aber großen, oder endlichen und noch nicht vollständig bekannten Daten erlaubt diese Art der Ausführung elegante Programme. So kann man etwa eine Transformation eines XML-Dokumentes als Folge von Transformationen des gesamten XML-Baumes beschreiben. Ausgeführt wird die Gesamttransformation aber von Beginn zum Ende des XML-Dokumentes, auch wenn das Ende noch gar nicht verfügbar ist.

Man beachte allerdings, dass Haskell nach Sprachdefinition lediglich nicht-strikt ist; die Bedarfsauswertung ist nur eine mögliche Implementierung der Nicht-Striktheit (die allerdings von allen gängigen Haskell-Übersetzern angewandt wird). Andere Implementierungen sind möglich (z.B. optimistic evaluation, Ennals & Peyton-Jones, ICFP'03).

Typsystem

• Haskell ist stark typisiert. Es wird also zum Beispiel streng zwischen Wahrheitswerten, Zeichen, ganzen Zahlen und Gleitkommazahlen unterschieden.

• Haskell erlaubt Typvariablen. Damit können Funktionen sehr allgemein formuliert werden. Wird eine allgemeingehaltene Funktion für bestimmte Typen verwendet, werden automatisch die Typen abgeglichen (Typinferenz).

Die Funktion map wendet eine beliebige Funktion auf die Elemente einer Liste an. Ihr Typ wird so angegeben:

 map :: (a -> b) -> [a] -> [b]

Wird map etwa mit der speziellen Funktion toUpper vom Typ Char -> Char aufgerufen, ergibt der Typabgleich

 map toUpper :: [Char] -> [Char]

• Haskell ist von der Grundidee her statisch typisiert, obwohl es auch Erweiterungen für dynamische Typen gibt. Das bedeutet, dass für die meisten Berechnungen die Typen bereits zum Zeitpunkt der Programmübersetzung feststehen. Dies deckt viele „offensichtliche“ Fehler noch vor Ausführung des Programms auf.

• Haskell unterstützt Funktionen höherer Ordnung (Funktionale). Das sind Funktionen, die Funktionen als Eingabeparameter bzw. Funktionen als Ergebnis haben. Ein Beispiel ist die map-Funktion, die eine Funktion f auf jedes Element eines Datentypes (hier Liste) anwendet.

 map :: (a -> b) -> [a] -> [b]
 map f [] = []
 map f (x:xs) = f x : map f xs

 map quadrat [1,2,3] = [quadrat 1, quadrat 2, quadrat 3] = [1,4,9]

• Funktionen erlauben Currying. Während man in anderen Sprachen Tupel als Argumente an Funktionen übergibt, also Funktionstypen der Form (a, b) -> c verwendet, ist in Haskell die Curry-Form a -> b -> c üblicher. Damit wird die partielle Auswertung von Funktionen möglich. Der Ausdruck map toUpper ist beispielsweise eine teilweise Auswertung von map, denn er beschreibt eine Funktion, nämlich die Funktion, welche alle Kleinbuchstaben einer Liste in Großbuchstaben verwandelt.

• Haskell erlaubt benutzerdefinierte Datentypen. Diese algebraischen Datentypen werden mit Hilfe von Datenkonstruktoren definiert.

 data Tree = Leaf Int | Branch Int Tree Tree

Das Beispiel zeigt die Datenstruktur eines mit ganzen Zahlen beschrifteten binären Baumes. Solch ein Baum Tree besteht entweder aus einem Blatt (Leaf Int) oder einer Verzweigung (Branch Int t1 t2), wobei t1 und t2 die Teilbäume darstellen, die wiederum die Struktur Tree haben. Zur Definition dieser Datenstruktur wurde sowohl der einstellige Konstruktor Leaf als auch der dreistellige Konstruktor Branch verwendet.

Datentypen mit mehreren ausschließlich parameterlosen Konstruktoren können als Aufzählungen eingesetzt werden.

 data Tag = Montag | Dienstag | Mittwoch | Donnerstag | Freitag | Samstag | Sonntag
    deriving (Show, Eq, Ord, Ix, Enum)

• Haskell unterstützt Typenklassen. Mit Typenklassen lassen sich Typen zusammenfassen, welche ähnliche Operationen unterstützen. In einer Signatur dürfen als Abstufung zwischen festen Typen wie Char und freien Typvariablen auch noch Typvariablen mit Einschränkung auf bestimmte Klassen verwendet werden.

Alle Ausprägungen einer Methode der Typklasse tragen den gleichen Namen. In gewisser Weise entsprechen Typklassen also dem Überladen von Funktionen. Der gleiche Funktionsname steht also abhängig vom Typ für verschiedene Funktionen. Zum Beispiel ist mit der ==-Methode der Klasse Eq der Vergleich sowohl zweier Zahlen als auch zweier Texte möglich. Trotzdem arbeitet der Gleichheitstest je nach Argumenttyp anders.

• In Haskell haben Ein- und Ausgabefunktionen einen speziellen Typkonstruktor namens IO.

  putStrLn :: String -> IO ()
  getLine  :: IO String

putStrLn gibt einen Text und einen Zeilenumbruch auf der Standardausgabe aus. Da es kein Ergebnis gibt, wird der leere Typ () als Rückgabetyp verwendet. getLine liest eine Textzeile von der Standardeingabe. Der IO-Typkonstruktor stellt sicher, dass man den Nutzern der Funktion offenlegen muss, dass die Ergebnisse durch Ein-/Ausgabe gewonnen wurden. Diese strenge Handhabung ermuntert Haskell-Programmierer zur klaren Trennung von Ein- und Ausgabe und anderen Teilen eines Programms. Der größte Teil eines Haskell-Programms besteht in der Regel aus Funktionen ohne Ein- und Ausgabe. Man kann IO-Typen natürlich auch in andere Typen einbetten und so zum Beispiel einen speziellen IO-Typ definieren, der nur Eingaben erlaubt.

Syntax

Haskell unterscheidet Groß- und Kleinschreibung. Bezeichner, die mit einem Großbuchstaben beginnen, stehen für Typen und Konstruktoren. Bezeichner, die mit einem Kleinbuchstaben beginnen, stehen für Typvariablen, Funktionen und Parameter.

Haskell bietet eine Reihe von syntaktischen Besonderheiten. Diese sollen nicht darüber hinwegtäuschen, dass alles rein funktional erklärt ist.

• Die do-Notation verleiht Berechnungen mit Monaden das Aussehen von imperativen Programmen.

Statt

 readFile "eingabe.txt" >>= writeFile "ausgabe.txt"

oder

 readFile "eingabe.txt" >>= (\inhalt -> writeFile "ausgabe.txt" inhalt)

kann man auch

 do inhalt <- readFile "eingabe.txt"
    writeFile "ausgabe.txt" inhalt

schreiben.

• Sowohl symbolische Bezeichner (bestehend etwa aus +, -, *, /, >, <) als auch alphanumerische Bezeichner (Buchstaben, Ziffern und Apostroph) können für Funktionen verwendet werden und sowohl als Infix-Operatoren als auch in Präfixschreibweise eingesetzt werden. Es gilt beispielsweise

 a + b      ==  (+) a b
 a `div` b  ==  div a b

• Haskell erlaubt eine Notation für die Listenverarbeitung (list comprehensions). Diese ist an die mathematische Schreibweise für Mengendefinitionen angelehnt. In folgendem Beispiel wird aus der Folge der natürlichen Zahlen die Folge der geraden Zahlen extrahiert.

 [ x | x <- [1..], even x]

als Umschreibung für

 filter even [1..]

Programmierung

• Haskell erlaubt Pattern Matching. So nennt man die Verwendung von Konstruktortermen als formale Parameter. Dabei sind die Parameterterme die Pattern (Muster) der Funktionsargumente.

 fak :: Integer -> Integer
 fak 0 = 1
 fak n = n * fak (n-1)

Die Funktion fak berechnet die Fakultät einer Zahl. Wird die Funktion mit 0 initialisiert, dann ergibt sich 1 als Ergebnis. Für alle anderen Fälle errechnet sich die Fakultät durch n*fak(n-1), wobei sich die Funktion rekursiv selbst aufruft. 0 und n sind die Muster (Pattern) von denen die Ergebnisbestimmung abhängt.

Module

Zu Haskell gehört auch ein Modulsystem. Der Haskell-98-Standard definiert eine Grundmenge von Modulen^[2], die ein standardkonformes Haskell-System zur Verfügung stellen muss. Beispielsweise ein Modul, welches Ein- und Ausgabe-Funktionen bereitstellt oder ein Modul, welches Funktionen auf Listen implementiert.

Um Module nutzen zu können, muss man sie importieren. Dies geschieht mithilfe des import Befehls.

 import List
 import Maybe

In verschiedenen Modulen können Funktionen und Typen die gleichen Namen besitzen. Diese Bezeichner können unterschieden werden,

• indem nur einer der Bezeichner importiert wird,

 import Data.List(delete)
 x = delete 'a' "abc"

• oder indem die Bezeichner qualifiziert, also durch Verbinden mit dem Modulnamen eindeutig gemacht werden.

 import qualified Data.List
 x = Data.List.delete 'a' "abc"

oder

 import qualified Data.List as List
 x = List.delete 'a' "abc"

Ebenfalls möglich aber nicht empfohlen ist das Ausblenden von Bezeichnern beim Importieren mit hiding.

Beispiele

Fakultät

Eine elegante Definition der Fakultätsfunktion, die Haskells Notation für Listen benutzt:

 fac :: Integer -> Integer
 fac n = product [1..n]

Fibonacci

Eine einfache Implementierung der Fibonacci-Funktion:

 fib :: Integer -> Integer
 fib 0 = 0
 fib 1 = 1
 fib n = fib (n - 2) + fib (n - 1)

Eine schnelle Implementierung der Folge:

 fibs :: [Integer]
 fibs = 0 : 1 : (zipWith (+) fibs (tail fibs))

tail entfernt das erste Element aus einer Liste, zipWith kombiniert zwei Listen elementweise mithilfe einer weiteren Funktion (hier (+)). Die Definition entspricht einer Fixpunktgleichung. Dass die Definition stimmt, überprüft man am schnellsten, indem man sich vorstellt, dass fibs bereits fertig berechnet vorliegt. Als nächstes muss man sich noch überlegen, dass die Definition auch ausgewertet werden kann. Die ersten beiden Glieder von fibs sind unmittelbar klar: 0 und 1. Für das Berechnen jedes weiteren Gliedes muss aber nur auf bereits berechnete Glieder von fibs zurückgegriffen werden. Die Bedarfsauswertung führt dazu, dass die Folge fibs tatsächlich elementweise berechnet wird.

Man könnte auch sagen, dass fibs ein Fixpunkt der Funktion \xs -> 0 : 1 : (zipWith (+) xs (tail xs)) ist. Das wiederum lässt sich in Haskell direkt notieren als

 fix (\xs -> 0 : 1 : (zipWith (+) xs (tail xs)))

Differenzengleichung

Man kann auf diese Weise sehr elegant Differentialgleichungen bezüglich Potenzreihen oder Differenzengleichung bezüglich Zahlenfolgen formulieren und gleichzeitig lösen.

Angenommen, man möchte die Differentialgleichung y'(x) = f(x,y(x)) bezüglich y in Form einer Zeitreihe lösen, also einer Liste von Zahlen. Durch diese Diskretisierung wird die Differentialgleichung zur Differenzengleichung. Statt eines Integrals berechnen wir Partialsummen. Die folgende Funktion hat als Parameter die Integrationskonstante und eine Zahlenfolge.

 integrate :: Num a => a -> [a] -> [a]
 integrate = scanl (+)

scanl akkumuliert die Werte einer Folge mit Hilfe einer anderen Funktion, hier (+), und gibt die Liste der Akkumulatorzustände zurück.

Damit kann man bereits das explizite Euler-Verfahren für die Schrittweite 1 implementieren. x0 und y0 sind hierbei die Anfangswerte. Der Apostroph hat keine eigenständige Bedeutung, er ist Teil des Namens y'.

 eulerExplicit :: Num a => (a -> a -> a) -> a -> a -> [a]
 eulerExplicit f x0 y0 =
    let x  = iterate (1+) x0
        y  = integrate y0 y'
        y' = zipWith f x y
    in  y

Diese Funktionsdefinition besteht also im wesentlichen aus der Feststellung, dass y das Integral von y' mit Anfangswert y0 ist, (oder umgekehrt, y' die Ableitung von y) und aus der eigentlichen Differentialgleichung y' = zipWith f x y. Weil man hierbei den Algorithmus eher in der Form der Aufgabenstellung als in Form eines Lösungsweges notiert, spricht man hierbei von Deklarativer Programmierung.

Quicksort

Der Quicksortalgorithmus, formuliert in Haskell:

 qsort :: Ord a => [a] -> [a]
 qsort []     = []
 qsort (x:xs) = qsort kleiner ++ [x] ++ qsort groesser
                where
                  kleiner  = [y | y <- xs, y < x]
                  groesser = [y | y <- xs, y >= x]

Die erste Zeile definiert die Signatur von Quicksort. Die zweite Zeile gibt an, dass die Funktion auf eine leere Liste angewendet wieder eine leere Liste ergeben soll. Die dritte Zeile sortiert rekursiv nicht-leere Listen: das erste Element x wird als mittleres Element der Ergebnisliste verwendet. Davor werden sortiert alle kleineren, dahinter alle größeren Elemente eingeordnet. Listenbeschreibungen werden dazu verwendet, aus der Restliste xs alle kleineren bzw. größeren Elemente als x auszuwählen.

Wie man es von Quicksort erwartet, besitzt auch diese Implementierung eine mittlere asymptotische Laufzeit von 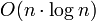$O(n \cdot \log n)$ und eine Worst-Case-Laufzeit von O(n²). Im Gegensatz zur geläufigen Implementierung in einer imperativen Sprache arbeitet dieses qsort jedoch nicht in-place.

Siehe auch

• International Conference on Functional Programming Contest
• Pugs (eine Perl 6-Implementierung in Haskell)

Einzelnachweise

1. ↑ Professor Paul Hudak's Home Page
2. ↑ http://www.haskell.org/onlinereport/

Literatur

• Why Functional Programming Matters by John Hughes, The Computer Journal, Vol. 32, No. 2, 1989, pp. 98 - 107. [1] Vorteile funktionaler Programmierung. Zeigt Formen der Modularisierung, die wesentlich auf Funktionen höherer Ordnung und Bedarfsauswertung beruhen.
• Simon Thompson: Haskell - The Craft of Functional Programming, 1999, Addison-Wesley, ISBN 0-201-34275-8
• Paul Hudak: The Haskell School of Expression - Learning Functional Programming Through Multimedia., 2000, Cambridge University Press, ISBN 0-521-64338-4
• Richard Bird: Introduction to Functional Programming using Haskell,second edition, Prentice Hall Europe 1998, ISBN 0-13-484346-0.

Weblinks

• http://www.haskell.org/ – zentrale Anlaufstelle zu der Programmiersprache Haskell mit Hinweisen zum Erlernen von Haskell
• http://www.informatik.uni-bonn.de/~ralf/teaching/Hskurs_toc.html – Haskell-Tutorial auf Deutsch
• http://haskell.readscheme.org/ – Bibliographie wissenschaftlicher Literatur zu Haskell