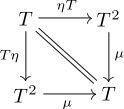Monade (Kategorientheorie)

Eine Monade ist im mathematischen Teilgebiet der Kategorientheorie eine Struktur, die gewisse formale Ähnlichkeit mit den Monoiden der Algebra aufweist.

Definition

Eine Monade ist ein Tripel (T,η,μ) aus

• einem Funktor T von einer Kategorie K in sich selbst, d.h.

  $T\colon K \to K$

• einer natürlichen Transformation $\eta\colon 1_K \to T$ (dabei steht 1_K für den Identitätsfunktor $K\to K$)
• einer natürlichen Transformation $\mu\colon T^2 \to T$ (dabei steht T² für $T\circ T$),

so dass die folgenden Bedingungen erfüllt sind:

• $\mu\circ T\mu = \mu \circ \mu T$, d. h. das folgende Diagramm kommutiert:

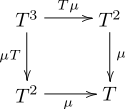
• $\mu\circ \eta T = \mu\circ T\eta = 1$, d. h. das folgende Diagramm kommutiert:

Explizit bedeutet die Kommutativität der Diagramme, dass für jedes Objekt X in K die beiden Diagramme

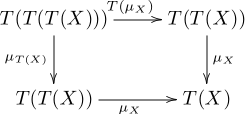
und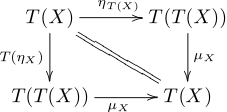

kommutieren. Die erste Bedingung ist analog zum Assoziativgesetz bei Monoiden, die zweite zur Existenz eines neutralen Elementes.

Beispiele

Adjungierte Funktoren

Ist ein Funktor $F\colon C\to D$ zu einem Funktor $G\colon D\to C$ linksadjungiert, und sind

$\eta\colon 1_C\to GF$ bzw. $\varepsilon\colon FG\to 1_D$

Einheit bzw. Koeinheit der Adjunktion, so ist (T,η,μ) mit

• $T=GF\colon C\to C$
• μ = GεF, also μ_X = G(ε_F(X)) für Objekte $X\in\mathrm{Ob}(C)$

eine Monade.

Dies ist im gewissen Sinn auch schon das einzige Beispiel, da jede Monade auf diese Weise entsteht, jedenfalls bis auf Isomorphie: Wir betrachten dazu für eine Monade (T,η,μ) die Kategorie K^T der sogenannten T-Algebren. Objekte dieser Kategorie sind Paare (X,α) wobei X ein Objekt von K und $\alpha: TX \to X$ ein Morphismus in K ist. Ein Morphismus $f: (X, \alpha) \to (Y,\beta)$ ist ein Morphismus $f: X \to Y$ in K so, dass $f \circ \alpha = \beta \circ Tf$ gilt. Wir haben Funktoren $G^T: K^T \to K$ - den Vergissfunktor, der die Zusatzstruktur vergisst - und $F^T: K \to K^T$ - den "freie Algebra"-Funktor - der auf Objekten durch F^T(X) = (TX,μ_X) und auf Morphismen durch F^T(f) = Tf wirkt (Tf ist wegen der Monadeneigenschaften wirklich ein Morphismus $(TX, \mu_X) \to (TY, \mu_Y)$). F^T und G^T sind adjungiert, die Einheit der Adjunktion ist durch die Einheit $\eta: 1 \to G^TF^T = T$ gegeben, die Koeinheit durch $\varepsilon_{(X,\alpha)} = \alpha: (TX, \mu_X) \to (X, \alpha)$. Die durch diese Adjunktion induzierte Monade (T,η,μ^T) ist gerade die Ausgangsmonade, denn wir haben

${\mu^T}_X = G^T(\varepsilon^T_{F^T(X)}) = G^T\bigl(\varepsilon^T_{(TX, \mu_X)}\bigr) = G^T(\mu_X) = \mu_X$.

Listen

Ein Beispiel für eine Monade sind Listen. Wenn [x₁,...,x_n] die Liste mit den Elementen x₁ bis x_n bezeichnet, dann stellt das folgende Tripel (T,η,μ) eine Monade über der Kategorie der Mengen dar:

1. Listen-Funktor:
   • Auf der Objektebene ergibt $T(X) = \{ [x_1, ..., x_n] \mid n\in\N, x_1, ..., x_n \in X \}$ die Menge aller Listen, deren Elemente aus X kommen, für eine beliebige Menge X.
   • Für eine Abbildung $f : X \to Y$ zwischen zwei Mengen ergibt T die entsprechende Abbildung $T(f) : T(X) \to T(Y)$ zwischen den Listenmengen mit T(f)([x₁,...,x_n]) = [f(x₁),...,f(x_n)]
2. Konstruktor für einelementige Listen: η_X(x) = [x]
3. Konkatenation von Listen: $\mu_X([l_1, ..., l_n]) = l_1 \cdot ... \cdot l_n$, also $\mu_X([[x_{11}, ... x_{1m_1}], ..., [x_{n1}, ..., x_{nm_n}]]) = [x_{11}, ... x_{1m_1}, ..., x_{n1}, ..., x_{nm_n}]$ - dies ist gewissermaßen das (einstufige) Flachklopfen einer Liste von Listen.

Die Aussage der Axiome lassen sich entsprechend auf das Listenbeispiel übertragen:

1. Wird das Axiom μTμ = μμT auf das Beispiel angewandt, ergibt sich für eine Menge X zunächst $\mu \circ \mu_{T(X)} = \mu \circ T(\mu_X)$. Auf das Listenbeispiel übertragen ergibt sich für $l \in T(T(T(X)))$ auch μ_X(μ_T(X)(l)) = μ_X(T(μ_X)(l))), d.h. dass es bei mehrfach verschachtelten Listen egal ist, ob von innen oder von außen flachgeklopft wird, was bei Listen offensichtlich erfüllt ist.
2. Das zweite Axiom sagt in diesem Beispiel aus, dass es beim Hinzufügen einer Listenebene egal ist, ob dies innen oder außen passiert, sofern danach flachgeklopft wird - es ist $\mu_X(\eta_{T(X)}([x_1, ..., x_n])) = \mu_X([[x_1, ..., x_n]]) = [x_1, ..., x_n] = \mu_X([[x_1], ..., [x_n]]) = \mu_X(T(\eta_X)([x_1, \dotsc, x_n]))$.

Diese Monade gehört zu einem adjungierten Funktorpaar F,G (wie oben) zwischen den Kategorien der Mengen bzw. Halbgruppen. F ordnet einer Menge die freie Halbgruppe über dieser Menge zu, G einer Halbgruppe die zugrundeliegende Menge.

Anwendung

Monaden werden u.a. in der Informatik in der funktionalen Programmierung verwendet, z.B. als Listen- oder IO-Monade in Haskell, siehe Monade (Informatik)

Literatur

• Saunders Mac Lane, Categories for the Working Mathematician. Springer-Verlag, Berlin 1971. ISBN 3-540-90035-7

Weblinks

• Lektion zu Monaden
• You Could Have Invented Monads! (And Maybe You Already Have.)
• Mehrteiliger Videokurs für Mathematiker (english)