- Ableitungsbaum
-
Ein Syntax-, Ableitungs- oder Parsebaum ist ein Begriff aus der theoretischen Informatik und bezeichnet eine baumförmige Darstellung einer Ableitung.
Man betrachte eine kontextfreie Grammatik
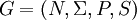 . Ein Ableitungsbaum dazu ist ein Baum, dessen Knoten mit Symbolen aus
. Ein Ableitungsbaum dazu ist ein Baum, dessen Knoten mit Symbolen aus 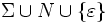 (also Terminal- und Nichtterminalsymbolen und dem leeren Wort) beschriftet sind. Der Baum ist geordnet, d. h. die Kinder jedes Knotens haben eine feste Reihenfolge, und für die Beschriftung gilt:
(also Terminal- und Nichtterminalsymbolen und dem leeren Wort) beschriftet sind. Der Baum ist geordnet, d. h. die Kinder jedes Knotens haben eine feste Reihenfolge, und für die Beschriftung gilt:- Die Wurzel ist mit dem Startsymbol S beschriftet. Diese Eigenschaft wird gelegentlich nicht verlangt. Ein Baum, der sie erfüllt, wird als vollständiger Ableitungsbaum bezeichnet.
- Wenn die Kinder eines mit A beschrifteten inneren Knotens mit den Symbolen z1,...,zm (in dieser Reihenfolge) beschriftet sind, muss die Grammatik die Regel
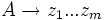 enthalten.
enthalten. - Die Blätter des Baumes sind mit Symbolen aus
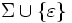 beschriftet.
beschriftet. - Ist ein Blatt mit
 gekennzeichnet, so ist es der einzige Nachfolger seines Vorgängerknotens.
gekennzeichnet, so ist es der einzige Nachfolger seines Vorgängerknotens.
Die inneren Knoten sind also genau die mit Nichtterminalsymbolen beschrifteten Knoten; die Blätter sind mit Terminalsymbolen oder dem leeren Wort beschriftet.
Zu einer gegebenen Ableitung ist der Ableitungsbaum eindeutig. Zu einem Ableitungsbaum können jedoch verschiedene Ableitungen existieren, je nachdem, in welcher Reihenfolge die Regeln angewendet werden (siehe dazu Rechtsableitung). Diese verschiedenen Ableitungen erzeugen jedoch alle dasselbe Wort, welches sich am Ableitungsbaum an den Blättern ablesen beziehungsweise durch eine Tiefensuche ermitteln lässt.
Verschiedene Ableitungen zu einem Ableitungsbaum bedeuten dabei noch nicht, dass die Grammatik mehrdeutig ist: Dazu muss es verschiedene Ableitungsbäume geben, die dasselbe Wort erzeugen.
In der Literatur kommt es vor, dass Syntax- und Ableitungsbaum nicht synonym verwendet werden. Insbesondere im Compilerbau ist der abstrakte Syntaxbaum von Bedeutung, der durch Entfernen von inneren Knoten mit nur einem Kind aus dem Ableitungsbaum hervorgeht. Der eigentliche Ableitungsbaum wird dabei zur Unterscheidung oft als konkreter Syntaxbaum oder Parsebaum bezeichnet.
Beispiel
Wir betrachten eine Grammatik mit dem Startsymbol S und den folgenden Regeln:
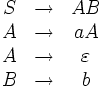
Ein möglicher Ableitungsbaum zu dieser Grammatik sieht so aus:
S / \ A B / \ \ a A b / \ a A \

Durch Ablesen der Terminalsymbole an den Blättern von links nach rechts erhält man das abgeleitete Wort aab. Ableitungen zu diesem Baum sind unter anderem die Linksableitung
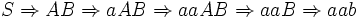
und die Rechtsableitung
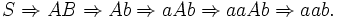
Wikimedia Foundation.
