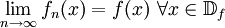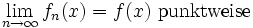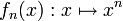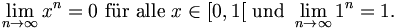Punktweise konvergent

In der Analysis ist punktweise Konvergenz die Eigenschaft einer Funktionenfolge f_n(x), für jedes Element x des Definitionsbereichs D_f gegen den Wert einer Grenzfunktion f(x) zu konvergieren, d.h.

$\lim_{n\rightarrow\infty}f_n(x)=f(x) \ \forall x \in \mathbb{D}_f$

Man schreibt dann

$\lim_{n\rightarrow\infty}f_n(x)=f(x)\ \mbox{punktweise}$

oder $f_n(x) \rightarrow_{pktw.} f(x)\ (n \rightarrow \infty).$

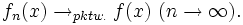
Formal konvergiert f_n also genau dann punktweise gegen f, wenn

$\forall x \in \mathbb{D}_f \ \forall \varepsilon > 0 \ \exists N \in \mathbb{N} \ \forall n \ge N : \left|f_n(x)-f(x)\right| < \varepsilon,$

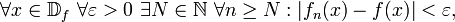
d.h. es muss für jedes x und für jedes ε > 0 eine natürliche Zahl N geben, so dass für alle 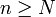$n\geq N$ gilt: $\left|f_n(x)-f(x)\right| < \varepsilon$.

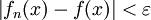Beispiel

Zum Beispiel konvergiert die Folge

$f_n(x) : x \mapsto x^n$

im Intervall [0,1] punktweise gegen die Funktion

$f(x) = \begin{cases} 0 & (x < 1) \\ 1 & (x=1) \end{cases}$,

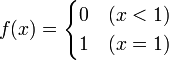denn offenbar gilt

$\lim_{n\rightarrow\infty}x^n = 0 \ \mbox{für alle}\ x \in [0, 1[ \ \mbox{und}\ \lim_{n\rightarrow\infty}1^n = 1.$

Abgrenzung

Es ist allerdings zu beachten, dass punktweise Konvergenz nicht gleichbedeutend mit gleichmäßiger Konvergenz ist, da z.B. das letzte oben genannte Beispiel zwar punktweise, keineswegs aber gleichmäßig konvergiert (so ist jedes Glied der Folge überall stetig differenzierbar, die Grenzfunktion allerdings nicht einmal stetig): Gleichmäßige Konvergenz ist eine wesentlich stärkere Aussage.

Für punktweise Konvergenz müssen die Werte der Funktionen f_n nicht unbedingt reelle Zahlen sein, sie können Elemente irgendeines Topologischen Raumes sein.