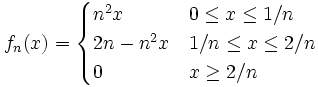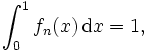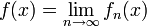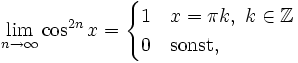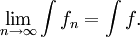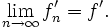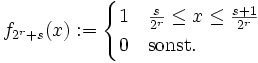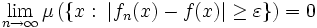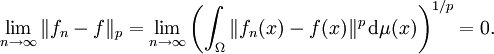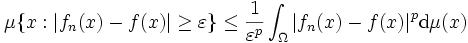- Funktionenreihe
-
Eine Funktionenfolge ist eine Folge, deren einzelne Glieder Funktionen sind. Funktionenfolgen und ihre Konvergenzeigenschaften sind für alle Teilgebiete der Analysis von großer Bedeutung. Vor allem wird hierbei untersucht, in welchem Sinne die Folge konvergiert, ob die Grenzfunktion Eigenschaften der Folge erbt oder ob Grenzwertbildungen bei Funktionenfolgen vertauscht werden können. Viele wichtige Beispiele sind Reihen von Funktionen, etwa Potenzreihen oder Fourier-Reihen.
Inhaltsverzeichnis
Definition
Eine (reelle) Funktionenfolge ist eine Folge
 von Funktionen
von Funktionen  . Allgemeiner können Definitions- und Zielmenge auch andere Mengen sein, beispielsweise Intervalle; sie müssen jedoch für alle Funktionen dieselben sein.
. Allgemeiner können Definitions- und Zielmenge auch andere Mengen sein, beispielsweise Intervalle; sie müssen jedoch für alle Funktionen dieselben sein.Abstrakt kann eine Funktionenfolge als Abbildung
für eine Definitionsmenge D und eine Zielmenge Z definiert werden.
Beispiele
Vertauschung Grenzwert und Integralzeichen
Für die Folge
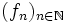 ,
, ![f_n\colon[0,1]\to\mathbb R](/pictures/dewiki/97/a89e6b47d052acd44389a8ecf9f3fc78.png) mit
mitgilt für jedes fixe x
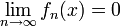 ,
,
sie konvergiert punktweise gegen die Nullfunktion. Jedoch gilt
also
Punktweise Konvergenz reicht also nicht aus, damit Grenzwert und Integralzeichen vertauscht werden dürfen; damit diese Vertauschung erlaubt ist, ist ein strengeres Konvergenzverhalten, nämlich die sogenannte gleichmäßige Konvergenz, notwendig.
Potenzreihen
In der Analysis treten Funktionenfolgen häufig als Summen von Funktionen, also als Reihe auf, insbesondere als Potenzreihe oder allgemeiner als Laurentreihe.
Fourieranalyse und Approximationstheorie
In der Approximationstheorie wird untersucht, wie gut sich Funktionen als Grenzwert von Funktionenfolgen darstellen lassen, wobei insbesondere die quantitative Abschätzung des Fehlers von Interesse ist. Die Funktionenfolgen treten dabei üblicherweise als Funktionenreihen auf, also als Summe
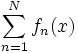 . Beispielsweise konvergieren Fourierreihen im L2-Sinn gegen die darzustellende Funktion. Bessere Approximationen im Sinne der gleichmäßigen Konvergenz erhält man oft mit Reihen aus Tschebyschow-Polynomen.
. Beispielsweise konvergieren Fourierreihen im L2-Sinn gegen die darzustellende Funktion. Bessere Approximationen im Sinne der gleichmäßigen Konvergenz erhält man oft mit Reihen aus Tschebyschow-Polynomen.Stochastik
In der Stochastik ist eine Zufallsvariable X als Funktion
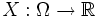 eines Maßraums (Ω,Σ,P) mit einem Wahrscheinlichkeitsmaß P(Ω) = 1 definiert. Folgen Xn von Zufallsvariablen sind daher spezielle Funktionenfolgen, ebenso sind Statistiken wie z. B. der Stichprobenmittelwert
eines Maßraums (Ω,Σ,P) mit einem Wahrscheinlichkeitsmaß P(Ω) = 1 definiert. Folgen Xn von Zufallsvariablen sind daher spezielle Funktionenfolgen, ebenso sind Statistiken wie z. B. der Stichprobenmittelwert  Funktionenfolgen. Wichtige Konvergenzeigenschaften dieser Funktionenfolgen sind z. B. die Gesetze der großen Zahlen oder die Zentralen Grenzwertsätze.
Funktionenfolgen. Wichtige Konvergenzeigenschaften dieser Funktionenfolgen sind z. B. die Gesetze der großen Zahlen oder die Zentralen Grenzwertsätze.Numerische Mathematik
In der numerischen Mathematik tauchen Funktionenfolgen beispielsweise bei der Lösung von partiellen Differentialgleichungen Df = 0 auf, wobei D ein (nicht notwendigerweise linearer) Differentialoperator und f die gesuchte Funktion ist. Bei der numerischen Lösung etwa mit der finiten Elementmethode erhält man Funktionen fn als Lösung der diskretisierten Version der Gleichung Dnf = 0, wobei n die Feinheit der Diskretisierung bezeichnet. Bei der Analyse des numerischen Algorithmus' werden nun die Eigenschaften der diskretisierten Lösungen fn, die eine Funktionenfolge bilden, untersucht; insbesondere ist es sinnvoll, dass die Folge der diskretisierten Lösungen fn bei Verfeinerung der Diskretisierung gegen die Lösung des Ausgangsproblems konvergiert.
Eigenschaften
Beschränktheit
Eine Funktionenfolge
 ist in einer Menge
ist in einer Menge 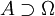 beschränkt, falls eine Konstante
beschränkt, falls eine Konstante  existiert, so dass
existiert, so dass 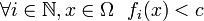 .
.lokal gleichmäßige Beschränktheit
Eine Funktionenfolge
 ist in einem offenen Gebiet
ist in einem offenen Gebiet 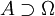 lokal gleichmäßig beschränkt, falls zu jedem offenen Gebiet Ω', mit
lokal gleichmäßig beschränkt, falls zu jedem offenen Gebiet Ω', mit  eine Konstante
eine Konstante  existiert, so dass
existiert, so dass 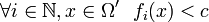 .
.Konvergenzbegriffe
Der Grenzwert f einer Funktionenfolge wird Grenzfunktion genannt. Da die in den Anwendungen auftretenden Funktionsfolgen sehr unterschiedliches Verhalten bei wachsendem Index haben können, ist es notwendig, sehr viele verschiedene Konvergenzbegriffe für Funktionenfolgen einzuführen. Von einem abstrakteren Standpunkt handelt es sich meist um die Konvergenz bezüglich gewisser Normen oder allgemeiner Topologien auf den entsprechenden Funktionenräumen; vereinzelt treten aber auch andere Konvergenzbegriffe auf.
Die verschiedenen Konvergenzbegriffe unterscheiden sich vor allem durch die implizierten Eigenschaften der Grenzfunktion. Die wichtigsten sind:
Klassische Konvergenzbegriffe
Punktweise Konvergenz
Existiert der punktweise Grenzwert
in jedem Punkt x des Definitionsbereiches, so wird die Funktionenfolge punktweise konvergent genannt. Beispielsweise gilt
die Grenzfunktion ist also unstetig.
Gleichmäßige Konvergenz
Eine Funktionenfolge (fn)n ist gleichmäßig konvergent gegen eine Funktion f, wenn die maximalen Unterschiede zwischen fn und f gegen null konvergieren. Dieser Konvergenzbegriff ist Konvergenz im Sinne der Supremumsnorm.
Gleichmäßige Konvergenz impliziert einige Eigenschaften der Grenzfunktion, wenn die Folgenglieder sie besitzen:
-
- Der gleichmäßige Limes stetiger Funktionen ist stetig.
- Der gleichmäßige Limes einer Folge integrierbarer Funktionen ist integrierbar, und das Integral der Grenzfunktion ist der Limes der Integrale der Folgenglieder: Ist (fn)n gleichmäßig konvergent gegen f, so gilt
- Konvergiert eine Folge (fn)n differenzierbarer Funktionen gleichmäßig gegen eine Funktion f, und ist auch die Folge der Ableitungen gleichmäßig konvergent, so ist auch f differenzierbar, und es gilt
Kompakte Konvergenz
Viele Reihen in der Funktionentheorie, insbesondere Potenzreihen, sind nicht gleichmäßig konvergent, weil die Konvergenz für zunehmende Argumente immer schlechter wird. Ein ähnlich guter Begriff ist der der kompakten Konvergenz, die gleichmäßige Konvergenz lediglich auf kompakten Teilmengen fordert. Da Stetigkeit eine lokale Eigenschaft ist, überträgt sie sich auch bei kompakter Konvergenz auf die Grenzfunktion.
Normale Konvergenz
In der Mathematik dient der Begriff der normalen Konvergenz der Charakterisierung von unendlichen Reihen von Funktionen. Eingeführt wurde der Begriff von dem französischen Mathematiker René Louis Baire.
Maßtheoretische Konvergenzbegriffe
Bei den maßtheoretischen Konvergenzbegriffen ist die Grenzfunktion üblicherweise nicht eindeutig, sondern nur fast überall eindeutig definiert. Alternativ lässt sich diese Konvergenz auch als Konvergenz von Äquivalenzklassen von Funktionen, die fast überall übereinstimmen, auffassen. Als eine solche Äquivalenzklasse ist dann der Grenzwert eindeutig bestimmt.
Punktweise Konvergenz fast überall
Sind ein Maßraum (Ω,Σ,μ) und eine Folge darauf messbarer Funktionen fn mit Definitionsmenge Ω gegeben, so wird die Funktionenfolge punktweise konvergent fast überall bezüglich μ genannt, wenn der punktweise Grenzwert
fast überall bezüglich μ existiert, wenn also eine Menge
 vom Maß Null (μ(Z) = 0) existiert, sodass fn eingeschränkt auf das Komplement
vom Maß Null (μ(Z) = 0) existiert, sodass fn eingeschränkt auf das Komplement 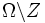 punktweise konvergiert.
punktweise konvergiert.Die Konvergenz fast überall bezüglich eines Wahrscheinlichkeitsmaßes wird in der Stochastik fast sichere Konvergenz genannt.
Beispielsweise gilt
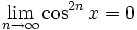 punktweise fast überall bezüglich des Lebesgue-Maßes.
punktweise fast überall bezüglich des Lebesgue-Maßes.
Ein anderes Beispiel ist die Funktionenfolge
![f_n: [0,1]\to[0,1]](/pictures/dewiki/51/363063992d0c492673e7458975e3a244.png) , wobei für
, wobei für 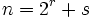 ,
, 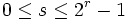
Diese Folge konvergiert für kein
![x\in[0,1]](/pictures/dewiki/99/c628ba2b1047de93f66cb815d986e107.png) , da sie für jedes fixe x die Werte 0 und 1 unenendlich oft annimmt. Für jede Teilfolge
, da sie für jedes fixe x die Werte 0 und 1 unenendlich oft annimmt. Für jede Teilfolge 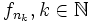 lässt sich aber eine Teilteilfolge
lässt sich aber eine Teilteilfolge 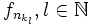 angegeben, sodass
angegeben, sodass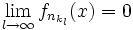 punktweise fast überall bezüglich des Lebesgue-Maßes.
punktweise fast überall bezüglich des Lebesgue-Maßes.
Gäbe es eine Topologie der punktweisen Konvergenz fast überall, so würde daraus, dass jede Teilfolge von fn eine Teilteilfolge enthält, die gegen 0 konvergiert, folgen, dass fn gegen 0 konvergieren muss. Da aber fn nicht konvergiert, kann es folglich keine Topologie der Konvergenz fast überall geben. Die punktweise Konvergenz fast überall ist damit ein Beispiel eines Konvergenzbegriffes, der zwar den Fréchet-Axiomen genügt, aber nicht durch eine Topologie erzeugt werden kann.[1]
Konvergenz dem Maße nach
In einem Maßraum (Ω,Σ,μ) wird eine Folge darauf messbarer Funktionen fn konvergent dem Maße nach gegen eine Funktion f genannt, wenn für jedes
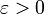
gilt [2].
In einem endlichen Maßraum, also wenn
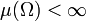 gilt, ist die Konvergenz dem Maße nach schwächer als die Konvergenz fast überall: Konvergiert eine Folge messbarer Funktionen fn fast überall gegen Funktion f, so konvergiert sie auch dem Maße nach gegen f [3].
gilt, ist die Konvergenz dem Maße nach schwächer als die Konvergenz fast überall: Konvergiert eine Folge messbarer Funktionen fn fast überall gegen Funktion f, so konvergiert sie auch dem Maße nach gegen f [3].In der Stochastik wird die Konvergenz dem Maße nach als Stochastische Konvergenz oder als Konvergenz in Wahrscheinlichkeit bezeichnet [4].
Lp-Konvergenz und Konvergenz in Sobolew-Räumen
Eine Funktionenfolge fn heißt Lp konvergent gegen f, wenn sie im Sinne des entsprechenden Lp-Raums
 konvergiert, wenn also
konvergiert, wenn alsoIst μ ein endliches Maß, gilt also
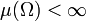 , so folgt für
, so folgt für 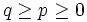 aus der Ungleichung der verallgemeinerten Mittelwerte, dass eine Konstante
aus der Ungleichung der verallgemeinerten Mittelwerte, dass eine Konstante  existiert, sodass
existiert, sodass 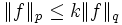 ; insbesondere folgt dann also aus der Lq-Konvergenz von fn gegen f auch die Lp-Konvergenz von fn gegen f.
; insbesondere folgt dann also aus der Lq-Konvergenz von fn gegen f auch die Lp-Konvergenz von fn gegen f.In der Stochastik wird die Lp-Konvergenz als Konvergenz im p-ten Mittel bezeichnet.
Aus der Lp-Konvergenz folgt die Konvergenz dem Maße nach, wie man aus der Tschebyschow-Ungleichung in der Form
sieht. [5]
Eine Verallgemeinerung der Lp-Konvergenz ist die Konvergenz in Sobolew-Räumen, die nicht nur die Konvergenz der Funktionswerte, sondern auch die Konvergenz der gewisser Ableitungen berücksichtigt. Der Sobolewschen Einbettungssatz beschreibt die Abhängigkeiten der Konvergenzbegriffe in den unterschiedlichen Sobolew-Räumen.
Fast gleichmäßige Konvergenz
In einem Maßraum (Ω,Σ,μ) wird eine Folge darauf messbarer reell- oder komplexwertiger Funktionen fn fast gleichmäßig konvergent gegen eine Funktion f genannt, wenn für jedes
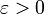 eine Menge
eine Menge 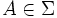 existiert, sodass
existiert, sodass 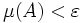 und fn auf dem Komplement
und fn auf dem Komplement  gleichmäßig gegen f konvergiert [6].
gleichmäßig gegen f konvergiert [6].Aus der fast gleichmäßigen Konvergenz folgt die punktweise Konvergenz fast überall [7]; aus dem Satz von Jegorow folgt, dass in einem endlichen Maßraum auch umgekehrt aus der punktweisen Konvergenz fast überall die fast gleichmäßige Konvergenz folgt [8]. In einem endlichen Maßraum, also insbesondere für reellwertige Zufallsvariablen, sind Konvergenz fast überall und fast gleichmäßige Konvergenz von reellwertigen Funktionenfolgen äquivalent.
Aus der fast gleichmäßigen Konvergenz folgt außerdem die Konvergenz dem Maße nach [7]. Umgekehrt gilt, dass eine dem Maße nach konvergente Folge eine Teilfolge enthält, die fast gleichmäßig (und damit auch fast überall) gegen die gleiche Grenzfolge konvergiert [9].
Schwache Konvergenz
Hierarchische Ordnung der Konvergenzbegriffe in Räumen mit endlichem Maß
In Maßräumen (Ω,Σ,μ) mit endlichem Maß, wenn also
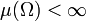 gilt, ist es großteils möglich, die unterschiedlichen Konvergenzbegriffe nach ihrer Stärke zu ordnen. Dies gilt insbesondere in Wahrscheinlichkeitsräumen, da dort ja μ(Ω) = 1 gilt.
gilt, ist es großteils möglich, die unterschiedlichen Konvergenzbegriffe nach ihrer Stärke zu ordnen. Dies gilt insbesondere in Wahrscheinlichkeitsräumen, da dort ja μ(Ω) = 1 gilt.Von der gleichmäßigen Konvergenz über die punktweise Konvergenz zur Konvergenz dem Maße nach
Aus der gleichmäßigen Konvergenz folgt die Konvergenz dem Maße nach auf zwei unterschiedlichen Wegen, der eine führt über die punktweise Konvergenz:
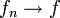 gleichmäßig
gleichmäßig 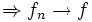 kompakt (d. h. gleichmäßig auf jeder kompakten Teilmenge).
kompakt (d. h. gleichmäßig auf jeder kompakten Teilmenge).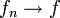 kompakt
kompakt 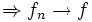 punktweise (jeder einzelne Punkt ist ja eine kompakte Teilmenge).
punktweise (jeder einzelne Punkt ist ja eine kompakte Teilmenge).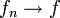 punktweise
punktweise 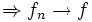 punktweise fast überall (bzw. fast sicher).
punktweise fast überall (bzw. fast sicher).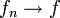 punktweise fast überall
punktweise fast überall 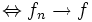 fast gleichmäßig.
fast gleichmäßig.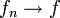 fast gleichmäßig
fast gleichmäßig 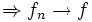 dem Maße nach (bzw. stochastisch oder in Wahrscheinlichkeit).
dem Maße nach (bzw. stochastisch oder in Wahrscheinlichkeit).
Von der gleichmäßigen Konvergenz über die Lp-Konvergenz zur Konvergenz dem Maße nach
Der andere Weg von der gleichmäßigen Konvergenz zur Konvergenz dem Maße nach führt über die Lp-Konvergenz:
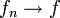 gleichmäßig
gleichmäßig 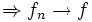 in
in 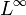 .
.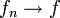 in
in 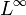
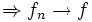 in Lp für alle reellen
in Lp für alle reellen 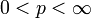 .
.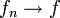 in Lp
in Lp 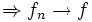 in Lq für alle reellen 0 < q < p.
in Lq für alle reellen 0 < q < p.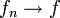 in Lp für
in Lp für  dem Maße nach (bzw. stochastisch oder in Wahrscheinlichkeit).
dem Maße nach (bzw. stochastisch oder in Wahrscheinlichkeit).
Von der Konvergenz dem Maße nach zur schwachen Konvergenz
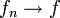 dem Maße nach
dem Maße nach 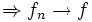 schwach (bzw. in Verteilung).
schwach (bzw. in Verteilung).
Wichtige Theoreme über Funktionenfolgen
- Satz von Arzelà-Ascoli
- Satz von Dini
- Auswahlsatz von Helly
- Satz von Jegorow
Quellen
- ↑ J. Cigler, H.-C. Reichel: Topologie. Eine Grundvorlesung. Bibliographisches Institut, Mannheim 1978. ISBN 3-411-00121-6. S. 88, Aufgabe 6
- ↑ A.N. Kolmogorow und S.V. Fomin: Reelle Funktionen und Funktionalanalysis. Deutscher Verlag der Wissenschaften, Berlin 1975, 5.4.6, Definition 4.
- ↑ A.N. Kolmogorow und S.V. Fomin: Reelle Funktionen und Funktionalanalysis. Deutscher Verlag der Wissenschaften, Berlin 1975, 5.4.6, Satz 7.
- ↑ Marek Fisz: Wahrscheinlichkeitsrechnung und mathematische Statistik. Deutscher Verlag der Wissenschaften, Berlin 1989, S 212
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Theorem 2.5.1.
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. S. 93.
- ↑ a b Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Theorem 2.5.2.
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Theorem 2.5.5.
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Theorem 2.5.3.
Literatur
- Heinz Bauer: Maß- und Integrationstheorie. 2. Auflage, De Gruyter, Berlin 1992, ISBN 3-11-013626-0 (Gebunden), ISBN 3-11-013625-2 (Broschiert), ab S.91 (§15 Konvergenzsätze) und ab S.128 (§20 Stochastische Konvergenz).
- Jürgen Elstrodt: Maß- und Integrationstheorie. 4. Auflage, Springer, Berlin 2005, ISBN 3-540-21390-2, (Beschreibt ausführlich die Zusammenhänge zwischen den verschiedenen Konvergenzarten).
Wikimedia Foundation.