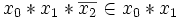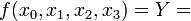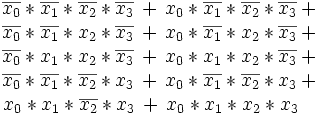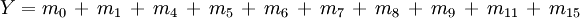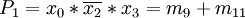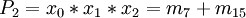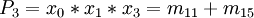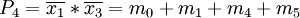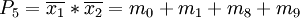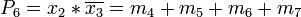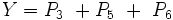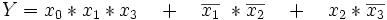QMCV

Das Verfahren nach Quine und McCluskey (QMCV, nach Willard Van Orman Quine und Edward J. McCluskey) ist eine Methode, um Boolesche Funktionen zu minimieren. Der Kern des Verfahrens wurde bereits von Quine vollständig beschrieben. Die Verfeinerungen von McCluskey betreffen im wesentlichen die praktische algorithmische Durchführbarkeit. Die Minimierung ist u. a. deshalb wichtig, weil dadurch die hardwaretechnische Realisierung einfacher und daher kostengünstiger wird. Der Vorteil dieses Verfahrens ist, dass es sich verhältnismäßig leicht in ein Computerprogramm fassen und so mittels eines Computers ausführen lässt. Das Verfahren benötigt im schlechtesten Fall exponentielle Laufzeit, um eine minimale Lösung zu finden. Das Verfahren findet immer eine minimale Lösung, es ist jedoch möglich, dass es noch andere (gleichwertige) Lösungen gibt, die nicht gefunden werden. Da das zugrunde liegende Problem NP-vollständig ist, und unter der Annahme, dass P!=NP gilt, gibt es kein in diesem Sinne effizientes Verfahren.

Das Verfahren bezieht sich zunächst nur auf Funktionsdarstellungen in kanonischer disjunktiver Normalform (KDNF). Ausdrücke in konjunktiver Normalform (KNF) lassen sich jedoch ohne weiteres über die Verneinung der betrachteten Funktion zunächst in eine DNF umwandeln, dann wie unten beschrieben minimieren und schließlich durch erneute Verneinung in eine KNF zurücktransformieren.

Beschreibung des Verfahrens

Grundprinzip

Das Grundprinzip des Quine-McCluskey-Verfahrens beruht auf der folgenden Eigenschaft von Konjunktionstermen: Unterscheiden sich zwei durch Disjunktion verknüpfte Konjunktionsterme nur durch die Negation einer einzigen Variablen, so kann man diese beiden Terme verschmelzen und dabei die betreffende Variable entfernen. Diese Eigenschaft erklärt sich aus folgendem algebraischen Zusammenhang:

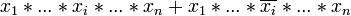
$x_1 * ... * x_i * ... * x_n + x_1 * ... * \overline{x_i}* ... * x_n$

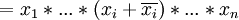
$= x_1 * ... * (x_i + \overline{x_i})* ... * x_n$

= x 1 * ... * x i - 1 * 1 * x i + 1 * ... * x n

= x 1 * ... * x i - 1 * x i + 1 * ... * x n

In diesem Zusammenhang ist es zweckmäßig, eine Boolesche Funktion unter dem Aspekt der Mengenlehre zu betrachten. (Es werden hier nur vollständig definierte Funktionen berücksichtigt):

Eine Boolesche Funktion ist als Menge von Konjunktionen aller unabhängigen Variablen darstellbar. Dies entspricht den Funktionswerten der Wahrheitstabelle und ist die Gesamtmenge. Für n unabhängige Variablen beträgt ihre Mächtigkeit $2 n$ Elemente.
Die Elemente werden hierbei auch Elementarkonjunktionen genannt. Dies ist also ein einzelner Funktionswert.
Diese Menge teilt sich in zwei Teilmengen auf. Ein Teil, welcher die Funktion zur wahren Aussage macht und ein Teil, welcher die Funktion nicht erfüllt. (Bei Verwendung von '0' und '1' also die Teilmenge der '1' und die Teilmenge der '0' in der Wahrheitstabelle).
Eine Konjunktion ist eine Teilmenge dieser Gesamtmenge. Es gibt $3 n$ mögliche Konjunktionen. (incl. der Gesamtmenge selbst).

Ein Element der Gesamtmenge ist Element einer Konjunktion, wenn die Belegung der in der Konjunktion enthaltenen Variablen mit den entsprechenden Werten des Elements (Elementarkonjunktion) die Konjunktion zur wahren Aussage macht.

Beispiel:

$x_0 * x_1 * \overline{x_2} \in x_0 * x_1$

$\overline{x_0} * x_1 * \overline{x_2} \in\!\!\!\!\!/\, x_0 * x_1$

Erstellen der kanonischen disjunktiven Normalform

Das Quine-McCluskey-Verfahren geht nun von einer algebraischen Darstellung der Formel in kanonischer disjunktiver Normalform (KDNF) aus. Eine solche KDNF besteht aus einer Disjunktion von Mintermen. Eine andere Darstellung muss also zuerst in diese Form gebracht werden.

Da in diesem Schritt unter Umständen bis zu $2 n$ Terme erzeugt werden, gibt es auch Varianten des Verfahrens, die nur eine DNF (statt einer KDNF) benötigen, wie z. B. die Resolventenmethode.

Ermitteln der Primterme

Alle Minterme werden jetzt nach aufsteigender Klasse sortiert, in einer Tabelle aufgelistet. Die Klasse einer Konjunktion ist die Anzahl der darin vorkommenden nicht negierten Variablen.

Man vergleicht nun alle Minterme benachbarter Klassen daraufhin, ob sie sich paarweise um eine einzige Negation unterscheiden. Ist dies der Fall, so verschmilzt man die beiden Terme zu einem neuen Term (der dann freilich kein Minterm mehr ist) und trägt ihn in eine zweite Tabelle ein. Die beiden verwendeten Terme werden (z. B. durch Abhaken) gekennzeichnet, sind aber auch weiterhin für Vergleiche heranzuziehen.

Auf die verschmolzenen Terme wendet man das Verfahren rekursiv in mehreren Stufen so lange an, bis keine weiteren Verschmelzungen mehr möglich sind. Es ist darauf zu achten, dass beide Terme (Tabellenzeilen) die gleichen Variablen enthalten. Während dieses Vorganges verbleiben einige Terme, die nicht verschmolzen werden konnten. Diese Terme bezeichnet man als Primterme bzw. Primkonjunktionen.

Hierbei treten ab der zweiten Minimierungsstufe die gleichen Konjunktionen mehrfach auf, sie sind jedoch nur einmal in die neue Tabelle einzutragen.

Erstellen der Primtermtabelle

Es ist durchaus möglich, dass nicht alle Primterme benötigt werden. Um herauszufinden, welche Primterme man unbedingt benötigt, erstellt man eine sogenannte Primtermtabelle. Als Spaltenköpfe der Tabelle werden die Minterme verwendet. Als Zeilenköpfe trägt man die Primterme ein. Die einzelnen Zellen der Tabelle sind also Kreuzungspunkte bestimmter Minterme mit bestimmten Primtermen.

Man trägt nun immer dann eine Markierung in der jeweiligen Zelle ein, wenn der Minterm Element des Primterms ist (s. o.).

Dominanzprüfung

Bei der Dominanzprüfung werden obsolete Zeilen und Spalten ermittelt.

Spaltendominanzprüfung

Die Spalten werden paarweise darauf verglichen, ob nicht eine Spalte existiert, in der die markierten Primterme eine Teilmenge der markierten Primterme der anderen Spalte sind. Ist dies der Fall, so kann die Spalte mit der Obermenge gestrichen werden, denn es müssen alle Konjunktionen erfasst werden und daher ist die Konjunktion mit der Obermenge durch Auswahl der Konjunktion mit der Teilmenge ebenfalls erfasst.

Beispiel:

In einer Tabelle stehen u. A. die beiden Spalten

K a = P 1 + P 2 + P 4

K b = P 1 + P 4

Hier kann $K a$ gestrichen werden, weil er von $K b$ vollständig dominiert wird. $K a$ ist daher obsolet und wird ab jetzt nicht mehr berücksichtigt.

Zeilendominanzprüfung

Jetzt vergleicht man die Zeilen (Primterme) der Tabelle paarweise, ob nicht eine Zeile existiert, in denen die markierten Minterme eine Teilmenge der markierten Minterme der anderen Zeile sind. Ist dies der Fall, so kann der Primterm mit der Teilmenge gestrichen werden, denn man kann für jede Markierung des gestrichenen Primterms den anderen Primterm als Ersatz nehmen. Die Relation ist hier also genau umgekehrt wie bei der Spaltendominanz.

Beispiel:

In einer Tabelle stehen u. A. die beiden Zeilen

P a = K 1 + K 2 + K 6 + K 7

P b = K 1 + K 2

Hier kann $P b$ gestrichen werden, weil er von $P a$ vollständig dominiert wird. $P b$ ist daher obsolet und wird ab jetzt nicht mehr berücksichtigt.

Diese beiden Prüfungen werden solange abwechselnd wiederholt, bis bei einer Prüfung keine Zeile/Spalte mehr gestrichen werden kann, mindestens jedoch je einmal.

Auswahl der Primterme

Die verbleibenden Primterme muss man jetzt so auswählen, dass alle Minterme abgedeckt werden. Hierfür kann es mehrere (ggf. gleichwertige) Möglichkeiten geben. Man wählt dabei möglichst wenige und kleine Primterme, da man ja eine optimierte Funktion erreichen möchte, die schließlich mit möglichst wenigen Schaltgattern technisch realisiert werden kann.

Beispiel

Es folgt ein Beispiel, um die Methode zu erklären:

Darstellung als kanonische disjunktive Normalform

Wir gehen von einer Booleschen Funktion $f$ mit vier Eingangsvariablen $x_0\dots x_3$ aus, deren kanonische disjunktive Normalform so aussieht:

$\, f(x_0 , x_1 , x_2 , x_3) = Y =$

$\begin{matrix} \\ \overline{x_0} * \overline{x_1} * \overline{x_2} * \overline{x_3} \, + \, {x_0} * \overline{x_1} * \overline{x_2} * \overline{x_3} \, + \, \\ \overline{x_0} * \overline{x_1} * {x_2} * \overline{x_3} \, + \, {x_0} * \overline{x_1} * {x_2} * \overline{x_3} \, + \, \\ \overline{x_0} * {x_1} * {x_2} * \overline{x_3} \, + \, {x_0} * {x_1} * {x_2} * \overline{x_3} \, + \, \\ \overline{x_0} * \overline{x_1} * \overline{x_2} * {x_3} \, + \, {x_0} * \overline{x_1} * \overline{x_2} * {x_3} \, + \, \\ {x_0} * {x_1} * \overline{x_2} * {x_3} \, + \, {x_0} * {x_1} * {x_2} * {x_3} \ \ \ \end{matrix}$

In anderer Schreibweise:

$Y = m_0 \, + \, m_1 \, + \, m_4 \, + \, m_5 \, + \, m_6 \, + \, m_7 \, + \, m_8 \, + \, m_9 \, + \, m_{11} \, + \, m_{15}$

Ermitteln der Primterme

Die Auswahltabellen

Die Ausgangstabelle:

Die erste Zusammenfassung ergibt:

Es dürfen nur Zeilen zusammengefasst werden, die die "-" an den gleichen Positionen haben (!)

Dritte Zusammenfassung

Tabelle 1
$m x$	$x 3$	$x 2$	$x 1$	$x 0$	OK

$m 0$	0	0	0	0	√

$m 1$	0	0	0	1	√
$m 4$	0	1	0	0	√
$m 8$	1	0	0	0	√

$m 5$	0	1	0	1	√
$m 6$	0	1	1	0	√
$m 9$	1	0	0	1	√

$m 7$	0	1	1	1	√
$m 11$	1	0	1	1	√

$m 15$	1	1	1	1	√

Tabelle 2
$m x + m y$	$x 3$	$x 2$	$x 1$	$x 0$	OK

$m 0 + m 1$	0	0	0	-	√
$m 0 + m 4$	0	-	0	0	√
$m 0 + m 8$	-	0	0	0	√

$m 1 + m 5$	0	-	0	1	√
$m 1 + m 9$	-	0	0	1	√
$m 4 + m 6$	0	1	-	0	√
$m 4 + m 5$	0	1	0	-	√
$m 8 + m 9$	1	0	0	-	√

$m 5 + m 7$	0	1	-	1	√
$m 6 + m 7$	0	1	1	-	√
$m 9 + m 11$	1	0	-	1	P₁

$m 7 + m 15$	-	1	1	1	P₂
$m 11 + m 15$	1	-	1	1	P₃

Tabelle 3
$m w + m x + m y + m z$	$x 3$	$x 2$	$x 1$	$x 0$	OK

$m 0 + m 1 + m 4 + m 5$	0	-	0	-	P₄
$m 0 + m 1 + m 8 + m 9$	-	0	0	-	P₅

$m 4 + m 6 + m 5 + m 7$	0	1	-	-	P₆

Keine weiteren Zusammenfassungen möglich.

Es ergeben sich daher sechs Primterme:

$\, P_1 = x_0 * \overline{x_2} * x_3 = m_9 + m_{11}$

$\, P_2 = x_0 * x_1 * x_2 = m_7 + m_{15}$

$\, P_3 = x_0 * x_1 * x_3 = m_{11} + m_{15}$

$\, P_4 = \overline{x_1} * \overline{x_3} = m_0 + m_1 + m_4 + m_5$

$\, P_5 = \overline{x_1} * \overline{x_2} = m_0 + m_1 + m_8 + m_9$

$\, P_6 = x_2 * \overline{x_3} = m_4 + m_5 + m_6 + m_7$

Erstellen der Primtermtabelle

Die Primtermtabelle sieht so aus:

	$m 0$	$m 1$	$m 4$	$m 5$	$m 6$	$m 7$	$m 8$	$m 9$	$m 11$	$m 15$
$P 1$								•	•
$P 2$						•				•
$P 3$									•	•
$P 4$	•	•	•	•
$P 5$	•	•					•	•
$P 6$			•	•	•	•

Dominanzprüfung

Die erste Spaltendominanzprüfung ergibt:

Streichen von $m 0$ , $m 1$ und $m 9$ wegen Spalte $m 8$
Streichen von $m 4$ , $m 5$ und $m 7$ wegen Spalte $m 6$

Danach sieht die Tabelle so aus:

	$m 6$	$m 8$	$m 11$	$m 15$
$P 1$			•
$P 2$				•
$P 3$			•	•
$P 4$
$P 5$		•
$P 6$	•

Die Zeilendominanzprüfung ergibt:

Streichen von $P 4$ (leer).
Streichen von $P 2$ wegen $P 3$
Streichen von $P 1$ wegen $P 3$

Somit erhält man:

	$m 6$	$m 8$	$m 11$	$m 15$
$P 3$			•	•
$P 5$		•
$P 6$	•

Eine Zweite Spaltendominanzprüfung ergibt:

Streichen von $m 15$ wegen $m 11$

Ergebnis:

	$m 6$	$m 8$	$m 11$
$P 3$			•
$P 5$		•
$P 6$	•

Eine zweite Zeilendominanzprüfung ergibt keine Streichungen mehr. Damit ist die Dominanzprüfung beendet.

Auswahl der Primterme

Die Auswahl geeigneter Primterme ist hier jetzt sehr einfach, da es nur eine Möglichkeit gibt: Benötigt werden die Primterme $P 3$ , $P 5$ und $P 6$ .

Verknüpfung der gewählten Primterme

Jetzt müssen die ausgewählten Primterme mittels Disjunktion zur Lösungsgleichung verknüpft werden:

$\, Y = P_3\ + P_5 \ + \ P_6$

$\, Y = x_0 * x_1 * x_3 \quad + \quad \overline{x_1}\ * \overline{x_2} \quad + \quad x_2 * \overline{x_3}$

Anmerkung

Das Problem, eine minimale Anzahl von Primtermen aus der Primtermtabelle auszuwählen, ist NP-vollständig; d.h., für viele Fälle ist kein wesentlich besseres Verfahren bekannt, als alle möglichen Auswahlen auszuprobieren. Deshalb bietet es sich an, das Minimum nur näherungsweise zu bestimmen. Beispielsweise wählt man zuerst die Spalten mit nur einer Markierung aus (diese sind zwingend notwendig), danach sucht man in den Spalten mit wenig Markierungen oder in Zeilen mit vielen Markierungen nach geeigneten Termen.

Das Verfahren hat insbesondere bei höherer Variablenzahl Vorteile gegenüber dem Karnaugh-Veitch-Diagramm (KVD). Als Faustregel gilt: Bis fünf Variablen ist das KVD besser, ab sechs Variablen das QMCV.

Weblinks

Wikimedia Foundation.

Игры ⚽ Поможем написать реферат

Schlagen Sie auch in anderen Wörterbüchern nach:

Bündelminimierung — Das Verfahren nach Quine und McCluskey (QMCV, nach Willard Van Orman Quine und Edward J. McCluskey) ist eine Methode, um Boolesche Funktionen zu minimieren. Der Kern des Verfahrens wurde bereits von Quine vollständig beschrieben. Die… … Deutsch Wikipedia
Quine-McCluskey-Verfahren — Das Verfahren nach Quine und McCluskey (QMCV, nach Willard Van Orman Quine und Edward J. McCluskey) ist eine Methode, um Boolesche Funktionen zu minimieren. Der Kern des Verfahrens wurde bereits von Quine vollständig beschrieben. Die… … Deutsch Wikipedia
Verfahren nach Quine und McCluskey — Das Verfahren nach Quine und McCluskey (QMCV, nach Willard Van Orman Quine und Edward J. McCluskey) ist eine Methode, um Boolesche Funktionen zu minimieren. Der Kern des Verfahrens wurde bereits von Quine vollständig beschrieben. Die… … Deutsch Wikipedia
Verfahren von Quine und McCluskey — Das Verfahren nach Quine und McCluskey (QMCV, nach Willard Van Orman Quine und Edward J. McCluskey) ist eine Methode, um Boolesche Funktionen zu minimieren. Der Kern des Verfahrens wurde bereits von Quine vollständig beschrieben. Die… … Deutsch Wikipedia

Academic dictionaries and encyclopedias

QMCV

Inhaltsverzeichnis

Beschreibung des Verfahrens

Grundprinzip

Erstellen der kanonischen disjunktiven Normalform

Ermitteln der Primterme

Erstellen der Primtermtabelle

Dominanzprüfung

Spaltendominanzprüfung

Zeilendominanzprüfung

Auswahl der Primterme

Beispiel

Darstellung als kanonische disjunktive Normalform

Ermitteln der Primterme

Erstellen der Primtermtabelle

Dominanzprüfung

Auswahl der Primterme

Verknüpfung der gewählten Primterme

Anmerkung

Weblinks

Schlagen Sie auch in anderen Wörterbüchern nach:

Share the article and excerpts

Academic dictionaries and encyclopedias

Deutsch Wikipedia

QMCV

Inhaltsverzeichnis

Beschreibung des Verfahrens

Grundprinzip

Erstellen der kanonischen disjunktiven Normalform

Ermitteln der Primterme

Erstellen der Primtermtabelle

Dominanzprüfung

Spaltendominanzprüfung

Zeilendominanzprüfung

Auswahl der Primterme

Beispiel

Darstellung als kanonische disjunktive Normalform

Ermitteln der Primterme

Erstellen der Primtermtabelle

Dominanzprüfung

Auswahl der Primterme

Verknüpfung der gewählten Primterme

Anmerkung

Weblinks

Schlagen Sie auch in anderen Wörterbüchern nach:

Share the article and excerpts

Direct link