Innenprodukt — Das Skalarprodukt (auch inneres Produkt oder Punktprodukt) ist eine mathematische Verknüpfung. Historisch wurde es zuerst für den euklidischen Raum eingeführt. Dort berechnet sich das Skalarprodukt zweier Vektoren und nach der Formel Dabei sind … Deutsch Wikipedia
Kanonisches Skalarprodukt — Das Skalarprodukt (auch inneres Produkt oder Punktprodukt) ist eine mathematische Verknüpfung. Historisch wurde es zuerst für den euklidischen Raum eingeführt. Dort berechnet sich das Skalarprodukt zweier Vektoren und nach der Formel Dabei sind … Deutsch Wikipedia
Punktprodukt — Das Skalarprodukt (auch inneres Produkt oder Punktprodukt) ist eine mathematische Verknüpfung. Historisch wurde es zuerst für den euklidischen Raum eingeführt. Dort berechnet sich das Skalarprodukt zweier Vektoren und nach der Formel Dabei sind … Deutsch Wikipedia
Signatur (Lineare Algebra) — Die Signatur (auch Sylvester Signatur) ist Eigenschaft einer symmetrischen Bilinearform, welche unabhängig von der Basiswahl im Vektorraum ist. Dies ist das Resultat des Trägheitssatzes von Sylvester. Haben also zwei Bilinearformen dieselbe… … Deutsch Wikipedia
Skalares Produkt — Das Skalarprodukt (auch inneres Produkt oder Punktprodukt) ist eine mathematische Verknüpfung. Historisch wurde es zuerst für den euklidischen Raum eingeführt. Dort berechnet sich das Skalarprodukt zweier Vektoren und nach der Formel Dabei sind … Deutsch Wikipedia
Standardskalarprodukt — Das Skalarprodukt (auch inneres Produkt oder Punktprodukt) ist eine mathematische Verknüpfung. Historisch wurde es zuerst für den euklidischen Raum eingeführt. Dort berechnet sich das Skalarprodukt zweier Vektoren und nach der Formel Dabei sind … Deutsch Wikipedia
Summenprodukt — Das Skalarprodukt (auch inneres Produkt oder Punktprodukt) ist eine mathematische Verknüpfung. Historisch wurde es zuerst für den euklidischen Raum eingeführt. Dort berechnet sich das Skalarprodukt zweier Vektoren und nach der Formel Dabei sind … Deutsch Wikipedia
Sylvester'scher Trägheitssatz — Der Trägheitssatz von Sylvester oder Sylvester scher Trägheitssatz benannt nach James Joseph Sylvester ist ein Resultat aus der linearen Algebra. Dieser Satz macht eine Aussage über Invarianten darstellender Matrizen von symmetrischen… … Deutsch Wikipedia
Sylvesterscher Trägheitssatz — Der Trägheitssatz von Sylvester oder Sylvester scher Trägheitssatz benannt nach James Joseph Sylvester ist ein Resultat aus der linearen Algebra. Dieser Satz macht eine Aussage über Invarianten darstellender Matrizen von symmetrischen… … Deutsch Wikipedia
Sylvester’scher Trägheitssatz — Der Trägheitssatz von Sylvester oder Sylvester scher Trägheitssatz benannt nach James Joseph Sylvester ist ein Resultat aus der linearen Algebra. Dieser Satz macht eine Aussage über Invarianten darstellender Matrizen von symmetrischen… … Deutsch Wikipedia
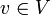 , für die S(v,w) = 0 für alle
, für die S(v,w) = 0 für alle 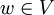 .
.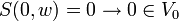 , sowie die Abgeschlossenheit gegenüber Addition und Multiplikation mit einem Skalar.
, sowie die Abgeschlossenheit gegenüber Addition und Multiplikation mit einem Skalar.