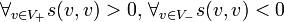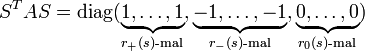Sylvester'scher Trägheitssatz

Der Trägheitssatz von Sylvester oder Sylvester'scher Trägheitssatz benannt nach James Joseph Sylvester ist ein Resultat aus der linearen Algebra. Dieser Satz macht eine Aussage über Invarianten darstellender Matrizen von symmetrischen Bilinearformen.

Aussage des Satzes

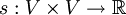Sei V ein endlichdimensionaler $\R$-Vektorraum mit einer symmetrischen Bilinearform $s: V \times V \rightarrow \R$. Der Ausartungsraum V₀ von V ist definiert als

$V_0 := \{v \in V: s(v,w) = 0\ \forall w \in V\}$.

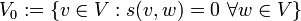Der sylvestersche Trägheitssatz besagt nun, dass eine direkte Zerlegung

$V = V_+ \oplus V_- \oplus V_0$

mit

$\forall_{v\in V_+}s(v,v)>0,\,\forall_{v\in V_-}s(v,v)<0$

existiert und dass hierbei die Zahlen 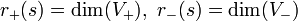$r_+(s) = \dim(V_+),\ r_-(s) = \dim(V_-)$ und r₀(s) = dim(V₀) (letztere trivialerweise) Invarianten von s sind, d.h. für alle solchen Zerlegungen gleich. Insbesondere ist

$r_+(s) = \max\{\dim(W) : W \subset V\ \mathrm{Untervektorraum\ und}\ \forall v \in W, v\neq 0 \to s(v,v) > 0 \}$.

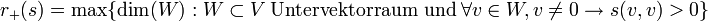Die analoge Aussage gilt auch für r ₋ (s).

Außerdem folgt aus der direkten Zerlegung sofort r ₊ (s) + r ₋ (s) + r₀(s) = dim(V).

Das Tripel σ(s) = (r ₊ (s),r ₋ (s),r₀(s)) heißt Trägheitsindex oder (Sylvester-)Signatur von V.

Folgerungen und Bemerkungen

• Aus dem Satz folgt, dass man zu einer gegebenen symmetrischen Bilinearform s mit den Invarianten r ₊ (s) und r ₋ (s) eine Basis existiert, sodass die darstellende Matrix von s die Diagonalform

$S^TAS=\operatorname{diag}(\underbrace{1,\ldots,1}_{r_+(s)\text{-mal}},\underbrace{-1,\ldots,-1}_{r_-(s)\text{-mal}},\underbrace{0,\ldots,0}_{r_0(s)\text{-mal}})$

besitzt.

• Seien 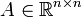$A \in \R^{n\times n}$ eine symmetrische Matrix und 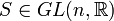$S \in GL(n,\R)$ eine invertierbare Matrix. So besagt eine zweite Folgerung aus dem Satz, dass A und S^TAS mit Vielfachheit gezählt die gleichen Anzahlen positiver und negativer Eigenwerte haben. Dies ist nicht trivial, denn die Eigenwerte einer quadratischen Matrix sind im Allgemeinen nur unter der Transformation SAS ^{− 1} invariant, nicht jedoch unter S^TAS.

• Der Trägheitssatz ist für hermitesche Bilinearformen bzw. hermitesche Matrizen nicht gültig. Eine hermitesche Matrix lässt sich dafür immer auf die Form 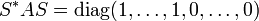$S^*AS=\operatorname{diag}(1,\dots,1,0,\dots,0)$ bringen.
  Hierbei bedeudet S^* die zu S hermitesch adjungierte Matrix.

Literatur

• Gerd Fischer: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-03217-0