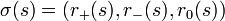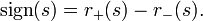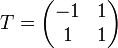Signatur (Lineare Algebra)

Die Signatur (auch Sylvester-Signatur) ist Eigenschaft einer symmetrischen Bilinearform, welche unabhängig von der Basiswahl im Vektorraum ist. Dies ist das Resultat des Trägheitssatzes von Sylvester. Haben also zwei Bilinearformen dieselbe Signatur, so beschreiben sie dieselbe Abbildung bezüglich unterschiedlicher Basen.

Definition

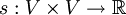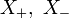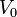Sei V ein endlichdimensionaler Vektorraum und $s: V \times V \rightarrow \R$ eine symmetrische Bilinearform. So seien $X_+,\ X_-$ und $V_0\;$ definiert durch

$X_+ := \{v \in V: s(v,v)>0\}$,

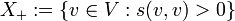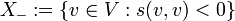$X_- := \{v \in V: s(v,v)<0\}$ bzw.

$V_0 := \{v \in V: s(v,w) = 0\ \forall w \in V\}$.

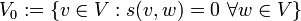Der Vektorraum V₀ heißt Ausartungsraum. X₊ und X_- sind (gewöhnlich) keine Vektorräume. Aber mit darin als Untermengen enthaltenen Vektorräumen maximaler Dimension

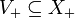$V_+ \subseteq X_+$ und $V_- \subseteq X_-$

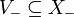
kann man eine direkte Zerlegung

$V = V_+ \oplus V_- \oplus V_0$

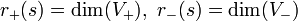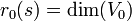erhalten. Das aus den Einträgen $r_+(s) = \dim(V_+),\ r_-(s) = \dim(V_-)$ und $r_0(s) = \dim(V_0)\;$ zusammengesetzte Tripel

$\sigma(s) = (r_+(s), r_-(s), r_0(s))\;$

heißt Trägheitsindex oder (Sylvester-)Signatur. Wegen der Zerlegungseigenschaft gilt

$r_+(s) + r_-(s) + r_0(s)) = \dim V\;$.

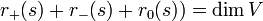Gelegentlich wird auch

$\operatorname{sign}(s)=r_+(s)-r_-(s).$

als Signatur bezeichnet, insbesondere, wenn keine Ausartung vorliegt, also $r_0(s) = 0\;$.

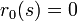Entsprechend definiert man diese Signaturen auc für nxn-Matrizen. Im Fall n=1 reproduziert die hier definierte sign-Funktion das gewöhnliche Vorzeichen für reelle Zahlen.

Beispiel

• Sei 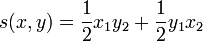$s(x,y) = \frac{1}{2}x_1y_2 + \frac{1}{2} y_1x_2$ eine symmetrische Bilinearform. So hat die darstellende Matrix der Kanonischen Basis die Form

$M_\mathcal{K}(s) = \begin{pmatrix} 0 & \frac{1}{2} \\ \frac{1}{2} & 0 \end{pmatrix}$.

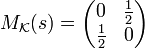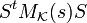Fasst man diese Matrix zwischenzeitlich als selbstadjungierten Endomorphismus von $\R^2$ auf, so weiß man auf Grund des Spektralsatzes, dass es eine Orthonormalbasis aus Eigenvektoren gibt, sodass $S^t M_\mathcal{K}(s) S$ Diagonalgestalt hat. Multipliziert man jeden Eigenvektor noch mit 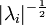$|\lambda_i|^{-\frac{1}{2}}$, wobei λ_i der entsprechende Eigenwert ist und führt dann die Basistransformation durch, so erhält man eine Diagonalmatrix mit Einträgen 1,-1 und 0 auf der Diagonalen. Hier kann man direkt die Signatur ablesen. 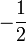In unserem konkreten Beispiel lauten die Eigenwerte $\frac{1}{2}$ und $-\frac{1}{2}$ und die orthonormalen Eigenvektoren 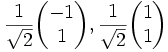$\frac{1}{\sqrt{2}}\begin{pmatrix} -1 \\ 1 \end{pmatrix}, \frac{1}{\sqrt{2}}\begin{pmatrix}1 \\ 1 \end{pmatrix}$. Multipliziert man diese Basis noch mit wie oben beschrieben mit 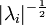$|\lambda_i|^{-\frac{1}{2}}$, so erhällt man als Transformationsmatrix

$T = \begin{pmatrix} -1 & 1 \\ 1 & 1 \end{pmatrix}$

und die Basistransformation sieht folgendermaßen aus

$T^t M_\mathcal{K}(s) T = \begin{pmatrix} -1 & 1 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} 0 & \frac{1}{2} \\ \frac{1}{2} & 0 \end{pmatrix} \begin{pmatrix} -1 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}$.

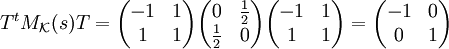Also hat die der Matrix zugeordnete Bilinearform die Signatur (1,1,0). Bei diesem Beispiel muss man allerdings beachten, dass Bilinearform keine Eigenwerte besitzen und dass der Weg über die Eigenwerte nur ein Trick zum Rechnen ist.

• Ein wichtiges Beispiel aus der Physik ist die Minkowski-Metrik der speziellen Relativitätstheorie. Dies ist eine symmetrische Bilinearform mit der Signatur (1,3,0).

Spezialfall

Gegeben ist eine symmetrische, nicht-singuläre Matrix. Dann ist die Signatur gegeben durch:

$\mathrm{sgn}(A) = \mathrm{sgn}(A_1) + v_g - v_a\;$.

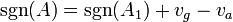Hierbei bezeichnet A₁ den ersten Hauptminor von A. Die beiden anderen Größen ergeben sich bei Berechnung der Determinanten der weiteren Minoren, wobei nur das Vorzeichen wichtig ist. v_g ist die Anzahl an gleichbleibenden Vorzeichen von det(A_k) nach det(A_{k + 1}) und v_a die Anzahl an Vorzeichenwechsel von det(A_k) nach det(A_{k + 1}).

Literatur

• Gerd Fischer: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-03217-0
• Mitschrieb Lineare Algebra 1 vom 22.01.2009