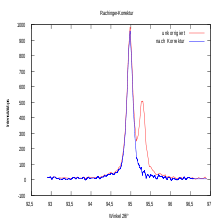
Rachinger-Korrektur

Die Rachinger-Korrektur ist ein von William Albert Rachinger (*1927) vorgeschlagenes und heute nicht mehr verwendetes rekursives Verfahren, um den störenden Kα₂-Peak aus einem Beugungsbild bei der Röntgenbeugung herauszurechnen.

Ursache des Doppelpeaks

Für Beugungsexperimente mit Röntgenstrahlung verwendet man in der Regel Strahlung mit der K_α-Wellenlänge des Anodenmaterials. Dabei handelt es sich jedoch um ein Dublett, also in Wirklichkeit um zwei geringfügig unterschiedliche Wellenlängen. Nach den Beugungsbedingungen der Laue- bzw. Bragg-Gleichung erzeugen beide Wellenlängen jeweils ein Intensitätsmaximum. Diese Maxima liegen sehr dicht beieinander, wobei ihr Abstand abhängig vom Beugungswinkel 2θ ist. Für größere Winkel ist der Abstand der Intentsitätsmaxima größer.

Vorgehen

Grundlagen

Die Wellenlängen der Kα₁- und Kα₂-Strahlung sind bekannt, damit auch ihre Energien über die Beziehung

$E = h \frac{c_0}{\lambda}.$

Daraus lässt sich für jeden Beugungswinkel der Winkelabstand Δθ der beiden Kα-Peaks bestimmen.

Weiterhin ist bekannt, wie sich die Intensitäten von Kα₁ und Kα₂ im Beugungsbild verhalten. Dieses Verhältnis ist quantenmechanisch festgelegt und beträgt für alle Anodenmaterialien:

$r = \frac{I_{\alpha_2}}{I_{\alpha_1}} = 0{,}5.$

Rechnung

Für die Rechnung geht man nun davon aus, dass sich beim Kα₂-Peak lediglich um eine mit dem Faktor r skalierte und um Δθ zu größeren Winkeln verschobene Variante des Kα₁-Peaks handelt.

Für die Gesamt-Intensität gilt also

I(θ) = I₁(θ) + I₂(θ),

wobei I₁(θ) die Intensität des reinen Kα₁-Peaks und I₂(θ) die Intensität des reinen Kα₂-Peaks ist. Mit dem oben genannten gilt jedoch für die Intensität des Kα₂-Peaks

$I_2(\theta) = r\cdot I_1(\theta-\Delta\theta)$,

so dass sich für die Gesamt-Intensität

$I(\theta) = I_1(\theta) + r\cdot I_1(\theta-\Delta\theta)$

ergibt.

Praktische Umsetzung

Beugungsbild vor und nach Rachinger-Korrektur

Um die Rachinger-Korrektur praktisch durchzuführen, beginnt man an einer steigenden Flanke eines Peaks. Für einen bestimmten Winkel θ wird die Intensität des Beugungsbildes I(θ) genommen und mit r skaliert zu $I'(\theta) = r\cdot I(\theta)$, gleichzeitig wird der Winkelunterschied Δθ berechnet. An der Stelle θ + Δθ kann die wahre Intensität I₁ (die vorläge, wenn es keinen Kα₂-Peak gäbe) berechnet werden durch

I₁(θ + Δθ) = I(θ + Δθ) − I'(θ).

Da die Messwerte von Röntgenbeugungsexperimenten in der Regel als ASCII-Tabellen vorliegen, kann dieses Vorgehen schrittweise wiederholt werden, bis das gesamte Beugungsbild durchgefahren wurde.

Heute wird diese Methode nicht mehr verwendet. Aufgrund der Leistungsfähigkeit der Computer wird der K_α2 - Peak einfach immer mitgefittet.

Einschränkungen

Aus der Art und Weise, wie das korrigierte Beugungsbild berechnet wird, ergibt sich, dass für die kleinen Beugungswinkel keine Korrektur erfolgt.

Literatur

• William Albert Rachinger: A Correction for the α1 α2 Doublet in the Measurement of Widths of X-ray Diffraction Lines. In: Journal of Scientific Instruments. 25, Nr. 7, 1948, S. 254–255.
• B. E. Warren, X-ray Diffraction. Dover Publications, 1969/1990, ISBN 0-486-66317-5