Radiant (Einheit)

Einheit
Norm	SI-Einheitensystem
Einheitenname	Radiant
Einheitenzeichen	rad
Beschriebene Größe(n)	ebener Winkel, Drehwinkel
Größensymbol(e)	α, β, γ, …1)
Dimensionsname	1 (dimensionslos)
In SI-Einheiten	$\mathrm{1\, rad = 1\, \frac{m}{m}} = 1$
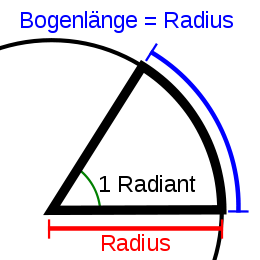
Siehe auch: Grad, Vollwinkel, Gon, Strich, Stunde, Prozent Anm. 1) alle kleinen griechischen Buchstaben außer π (Pi ist ein vorgegebener Wert, die Kreiszahl Pi)

Der Radiant (Einheitenzeichen: rad) dient zur Angabe der Größe eines ebenen Winkels. Er ist eine abgeleitete Einheit im SI-Einheitensystem. Der ebene Winkel von 1 Radiant umschließt auf der Umfangslinie eines Kreises mit 1 Meter Radius einen Bogen der Länge 1 Meter. Der Vollwinkel umfasst 2π Radiant: 1 Vollwinkel = 2 π rad.

Radiant im SI

Im Internationalen Einheitensystem (SI) ist Radiant der besondere Name für die dimensionslose, kohärente, abgeleitete SI-Einheit m/m. Aufgrund dieser Eigenschaften kann er in Rechnungen auch einfach durch 1 ersetzt werden, d. h. 1 rad = 1. Er kann auch mit den SI-Präfixen kombiniert werden, z. B. als Milliradiant (mrad) ^[1]. Durch das nicht notwendige, aber bewusst vorgenommene Hinzufügen des Einheitenzeichens rad in Größenwerten lässt sich in manchen Fällen darauf hinweisen, welche physikalische Größe gemeint ist, ohne sie namentlich anzugeben.

Beispiel:

Größe	Einheit
Arbeit	Nm
Drehmoment	Nm rad

Den Unterschied zwischen diesen Größen zeigt die Formel: Arbeit = Drehmoment * (gedrehter) Winkel. Mit dem Größenwert 5,25 Nmrad ist dann augenscheinlich ein Drehmoment, aber keine Arbeit gemeint, mit 5,25 Nm kann beides gemeint sein. Die Bezeichnung "Nmrad" ist allerdings in der Praxis unüblich, da sich die Differenzierung zwischen Arbeit und Drehmoment bereits aus der Thematik ergibt.

Umrechnung zwischen Radiant und Grad

Chart zur Umrechnung zwischen Radiant und Grad

Häufig benötigte Werte:

Grad	Radiant
$0^\circ$	0
$45^\circ$	$\frac{1}{4} \pi$
$57^\circ\, 17'\, 44''$	$\approx 1$
$57{,}29577951^\circ$
$90^\circ$	$\frac{1}{2} \pi$
$180^\circ$	π
$270^\circ$	$\frac{3}{2}\pi$
$360^\circ$	2π
3,44'	1mrad
0,206''	1μrad

Der Vollwinkel hat 2 π Radiant oder 360 Grad; daher gilt:

$2\pi\,\mathrm{rad} = 360^\circ$

$1\,\mathrm{rad} = \frac {360^\circ} {2 \pi} = \frac {180^\circ} {\pi} \approx 57{,}29577951^\circ$

oder:

$360^\circ = 2\pi\,\mathrm{rad}$

$1^\circ = \frac{2\pi}{360}\,\mathrm{rad} = \frac{\pi}{180}\,\mathrm{rad} \approx 0{,}017453293\,\mathrm{rad}$

Der Faktor für die Umrechnung von Radiant auf Grad ist also $\frac{180^\circ}{\pi} \ \left(= 1\,\mathrm{rad} = 1\right)$

Beispiele:

• $\alpha = \frac{3}{2}\,\pi\,\mathrm{rad} = \frac{3}{2}\,\pi \cdot \frac{180^\circ}{\pi} = \frac{3}{2} \cdot 180^\circ = 270^\circ$

• $\beta = 45^\circ = 45^\circ \cdot \frac{\pi}{\displaystyle 180^{\circ}} = \frac{\pi}{4} = \frac{\pi}{4}\,\mathrm{rad}$

Umrechnung zwischen Radiant und anderen Winkelmaßen

Hierfür ersetzt man in den obigen Formeln die Zahl „360“ durch die entsprechende Zahl des Vollwinkels im anderen Winkelmaß, die Zahl „180“ entsprechend durch die Hälfte des Vollwinkels. Also statt $\frac{180^\circ}{\pi}$ dann $\frac{200 \mathrm{gon}}{\pi}$ bzw. $\frac{12^h}{\pi}$ bzw. $\frac{16^-}{\pi}$ .

Taschenrechner und Computer

Wissenschaftliche Taschenrechner berechnen Winkelfunktionen wahlweise in Radiant oder in Grad, manchmal zusätzlich auch in Gon. Der Modus zur Berechnung in Radiant ist auf den meisten Taschenrechnern mit „RAD“ oder "R" gekennzeichnet.

In mathematischen Bibliotheken für Programmiersprachen verwenden die Winkelfunktionen stets das Bogenmaß. Um Gradangaben zu erhalten, müssen die obenstehenden Umrechnungsformeln angewandt werden.

Historisches

Im SI war zunächst offen gelassen worden, ob Radiant und Steradiant abgeleitete Einheiten oder Basiseinheiten sind; für beide wurde die Klasse der „ergänzenden Einheiten“ geschaffen. 1980 empfahl das CIPM, diese ergänzenden Einheiten als abgeleitete zu interpretieren. Dem folgte 1995 die 20. CGPM und beschloss in Resolution 8 die Aufhebung der Klasse der ergänzenden Einheiten.

Siehe auch

• Winkelmaß

Quellen

1. ↑ BIPM – SI-Broschüre, 8. Auflage, März 2006, Abschnitt 2.2.2, Tabelle 3: Kohärente abgeleitete SI-Einheiten mit besonderen Namen und Symbolen. [1]

Weblinks

 Commons: Radiant – Sammlung von Bildern, Videos und Audiodateien