- Relativ innerer Punkt
-
Der Begriff Relativ Innerer Punkt ist ein topologischer Begriff, der in der Mathematischen Optimierung gebraucht wird.
Inhaltsverzeichnis
Definition
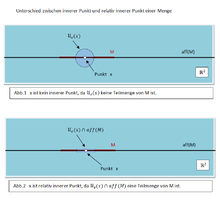
Es sei M eine Teilmenge eines n-dimensionalen reellen Vektorraums V, aff(M) die affine Hülle von M in V. Dann heißt ein Punkt x aus M relativ innerer Punkt von M, wenn es in dem affinen Raum aff(M), versehen mit der Unterraumtopologie, eine Umgebung von x gibt, die ganz in M enthalten ist.
Beispiele
Quader
Wir betrachten einen Quader im dreidimensionalen (reellen) Raum. Dann gilt:
- Ein Punkt im Inneren des Quaders ist relativ innerer Punkt des Vollquaders.
- Ein Punkt auf einer Seitenfläche des Quaders (nicht auf einer Kante) ist relativ innerer Punkt der betreffenden Seitenfläche, aber nicht des Vollquaders.
- Ein Punkt auf einer Kante des Quaders, der kein Eckpunkt des Quaders ist, ist relativ innerer Punkt der betreffenden Kante, aber weder einer Seitenfläche noch des Vollquaders.
- Ein Eckpunkt des Quaders ist in keiner (nichttrivialen) Teilmenge des Quaders ein relativ innerer Punkt.
Kreisscheibe
Wir betrachten eine abgeschlossene Kreisscheibe im dreidimensionalen (reellen) Raum. Dann gilt:
- Die affine Hülle der Kreisscheibe ist die Ebene im Raum, in der der Kreis liegt.
- Die Punkte der Kreislinie sind für die Kreisscheibe keine relativ inneren Punkte.
- Alle anderen Punkte der Kreisscheibe sind relativ innere Punkte.
Kurve in der Ebene
Sei C eine Kurve in der Ebene. Formal: C sei das Bild einer stetigen Funktion
 auf einem Intervall
auf einem Intervall  .
.Ein Punkt f(t) auf der Kurve, der weder ihr Anfangs- noch ihr Endpunkt ist (d.h. t liegt im Inneren von I ), ist genau dann ein relativ innerer Punkt der Kurve, wenn die Kurve in einer Umgebung von t geradeaus geht. Falls die Funktion f an der Stelle t zweimal differenzierbar ist, bedeutet dies, dass die Kurve dort die Krümmung 0 hat).
Kategorie:- Mengentheoretische Topologie
Wikimedia Foundation.