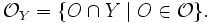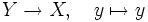- Unterraumtopologie
-
Im mathematischen Teilgebiet der Topologie versteht man unter der Teilraumtopologie (auch induzierten Topologie, relative Topologie, Spurtopologie oder Unterraumtopologie) die natürliche Struktur, die eine Teilmenge eines topologischen Raumes "erbt". Die Teilraumtopologie ist eine spezielle Initialtopologie.
Formale Definition
Es sei X die Grundmenge eines topologischen Raums
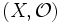 und
und 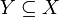 eine Teilmenge. Dann ist die Teilraumtopologie auf Y die Topologie
eine Teilmenge. Dann ist die Teilraumtopologie auf Y die TopologieDie offenen Teilmengen von Y sind also genau die Schnitte der offenen Teilmengen von X mit Y.
Eigenschaften
- Die Teilraumtopologie auf einer Teilmenge
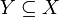 eines topologischen Raumes X ist die schwächste Topologie, für die die Inklusionsabbildung
eines topologischen Raumes X ist die schwächste Topologie, für die die Inklusionsabbildung
-
- stetig ist.
- Ist Y eine offene Teilmenge eines topologischen Raumes X so ist eine Teilmenge
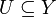 genau dann offen in der Teilraumtopologie von Y, wenn U als Teilmenge von X offen ist.
genau dann offen in der Teilraumtopologie von Y, wenn U als Teilmenge von X offen ist. - Ist Y eine abgeschlossene Teilmenge eines topologischen Raumes X, so ist eine Teilmenge
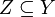 genau dann abgeschlossen in der Teilraumtopologie von Y, wenn Z als Teilmenge von X abgeschlossen ist.
genau dann abgeschlossen in der Teilraumtopologie von Y, wenn Z als Teilmenge von X abgeschlossen ist. - Eine stetige Abbildung topologischer Räume ist genau dann ein Monomorphismus im Sinne der Kategorientheorie, wenn sie als Abbildung auf das mit der Teilraumtopologie versehene mengentheoretische Bild ein Homöomorphismus ist. Insbesondere sind Monomorphismen injektiv.
Beispiele
- Man stelle sich ein Blatt Papier ohne Rand als zweidimensionales Objekt vor. Im
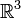 ist dies keine offene Menge. Betrachtet man aber die Topologie bezüglich der Ebene, in der sich das Blatt befindet, so liegt eine offene Menge vor.
ist dies keine offene Menge. Betrachtet man aber die Topologie bezüglich der Ebene, in der sich das Blatt befindet, so liegt eine offene Menge vor. - Die Teilraumtopologie auf
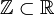 ist die diskrete Topologie, d.h. alle Teilmengen von
ist die diskrete Topologie, d.h. alle Teilmengen von 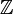 sind offen als Teilmengen des topologischen Raumes
sind offen als Teilmengen des topologischen Raumes 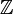 . Beispielsweise ist die Menge {0} eine offene Teilmenge von
. Beispielsweise ist die Menge {0} eine offene Teilmenge von 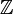 , weil sie Schnitt der offenen Teilmenge
, weil sie Schnitt der offenen Teilmenge 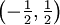 von
von  mit
mit 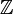 ist.
ist.
Wikimedia Foundation.