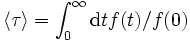Relaxierung

Relaxation bezeichnet die Entspannung nach einer Anspannung. Stabile physikalische Systeme kehren nach einer äußeren Störung über Relaxationsprozesse in ihren Grundzustand zurück.

Als Relaxationszeit bezeichnet man eine Zeitkonstante, die für einen gegebenen Relaxationsprozess charakteristisch ist. Wenn die Relaxation einer Größe f(t) einem exponentiellen Gesetz

f(t) = exp( − t / τ) * f(t = 0)

folgt, dann ist τ die zugehörige Relaxationszeit. Im Falle komplizierterer (zum Beispiel gestreckt-exponentieller) Zeitabhängigkeiten kann man die Relaxationszeit als

$\langle\tau\rangle = \int_0^\infty {\rm d}t f(t)/f(0)$

definieren.

In der Festigkeitslehre versteht man unter Relaxation eine Abnahme der Spannung bei konstanter Dehnung (z. B. erschlaffende Schraubenfeder bei konstanter Federstrecke).

---

Für spezifische Information zu einzelnen Relaxationsprozessen siehe

• im Straßenbau:
  • Relaxation von Asphalt und Bitumen
• in der Physik:
  • Relaxation (NMR) in der Kernspinresonanz („Spin-Spin-Relaxation“, „Spin-Gitter-Relaxation“)
  • Relaxation (Hydrodynamik)
  • Violent Relaxation (eines Sterngases oder Galaxienhaufens)
• in der Chemie:
  • Relaxationszeit einer Reaktion
• in Biologie / Medizin:
  • Muskelrelaxation
• im Operations Research (Relaxierung):
  • Das Weglassen von Bedingungen in Optimierungsmodellen, um ein einfacher lösbares Modell zu erhalten, welches das ursprüngliche Problem enthält.
    • Bei der LP-Relaxierung wird beispielsweise ein gemischt-ganzzahliges Optimierungsproblem dadurch relaxiert, dass die Ganzzahligkeitsforderung ignoriert wird.
    • Bei der Lagrange-Relaxierung werden Nebenbedingungen mit Strafkosten für deren Verletzung in die Zielfunktion aufgenommen.
• In der Numerischen Mathematik dient die Relaxation bei der Lösung von komplexen Gleichungssystemen, die mit Iterationsverfahren gelöst werden, als Hilfsmittel.

Weblinks

• longitudinale Relaxationszeit – dargestellt in einer Animation