Iterationsverfahren

Die Iteration (v. lat. iterare „wiederholen“) ist ein Begriff, der in verschiedenen Wissenschaften oder Anwendungsbereichen verwendet wird: Maschinenbau, Informatik, Linguistik, numerische Mathematik, Softwaretechnik, Geschichtswissenschaft und Philosophie.

Numerische Mathematik

In der numerischen Mathematik bezeichnet er eine Methode, sich der Lösung eines Rechenproblems schrittweise, aber zielgerichtet anzunähern (sukzessive Approximation). Sie besteht in der wiederholten Anwendung desselben Rechenverfahrens.

Meistens iteriert man mit Rückkopplung: Die Ergebnisse eines Iterationsschrittes werden als Ausgangswerte des jeweils nächsten Schrittes genommen – bis das Ergebnis (beziehungsweise Veränderung einer Bestandsgröße) zufrieden stellt. Ein Beispiel dafür ist das Newton-Verfahren. Manchmal setzt man den nächsten Schritt aus den Ergebnissen der vorherigen zwei Schritte (oder vor noch mehr Schritten) an, zum Beispiel bei der Regula Falsi.

Es muss anschließend noch bewiesen werden, dass die Iterationsfolge konvergiert und dass der Grenzwert mit der gesuchten Lösung übereinstimmt. Die Geschwindigkeit der Konvergenz ist ein Maß dafür, wie brauchbar die Iterationsmethode ist.

Anwendung der Methode

• Iteration wird angewandt in Fällen, in denen das Ergebnis sich nicht in geschlossener Form berechnen lässt, zum Beispiel bei der Kepler-Gleichung oder allgemeiner bei Optimierungsverfahren, oder wenn nachgebessert werden muss (Gleichungssysteme);
• Bei Anwendungsproblemen können die Eingabedaten fehlerbehaftet sein, dann ist die „exakte Lösung“ des gegebenen Problems nicht notwendigerweise besser als ihre Approximation. Das Iterationsverfahren wird bevorzugt, wenn es eine gute Näherung schneller liefert, als die Berechnung der exakten Lösung braucht.
• Manche Funktionen auf Taschenrechnern oder Fraktale werden beispielsweise iterativ berechnet.

Beispiel: Lösung einer Gleichung

Die Nullstelle einer Gleichung ist iterativ oft rascher gefunden als exakte, geschlossene Formeln:

1. Probieren, wo die Nullstelle von y = f(x) ungefähr liegt
2. zweimalige Berechnung von y mit x₁ und x₂
3. besserer Wert x₃ mit der Regula Falsi, die ein annähernd gerades Kurvenstück annimmt:
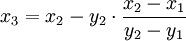4. $x_3 = x_2 - y_2 \cdot \frac{x_2 - x_1}{y_2 - y_1}$ und wiederholen, bis es genau genug ist.

Effizienz versus Eleganz

Als Algorithmus ist die Iteration oft effizienter als der elegantere rekursive Weg.

Informatik

Neben der mathematischen iterativen Problemlösung wird in der Informatik auch von Iteration gesprochen, wenn ein Zugriff iterativ, das heißt schrittweise, beziehungsweise wiederholt, auf Datenstrukturen erfolgt, beispielsweise bei einer FOR-Schleife. Hierbei steht der Begriff Datenstruktur für Sammlungen von Objekten, Objektreferenzen oder Datentypen. Der Zeiger auf diese Objekte nennt sich Iterator. In der Regel handelt es sich um Arrays, Listen, Schlüssel-Wert-Paare (Maps, Hashes) oder Mengen (Sets).

Siehe auch: Iterative Programmierung

Linguistik

Die sprachliche Iteration bezeichnet die Wiederholung von Wortteilen wie bei Ururgroßmutter.

Softwaretechnik

In der Softwaretechnik bezeichnet eine Iteration einen einzelnen Entwicklungszyklus, je nach Vorgehensmodell beginnend mit Planung, Analyse oder Entwurf, endend mit Implementierung, Test oder Wartung. Eine besondere Rolle spielen Iterationen beim Extreme Programming und beim Rational Unified Process.

Geschichtswissenschaft

In der Geschichtswissenschaft bezeichnet der Begriff die wiederholte Ausübung desselben Amtes in der Ämterlaufbahn der römischen Republik. Nach dem Mos maiorum war die Iteration verpönt. Beim Konsulat kam die mehrfache, in Ausnahmefällen auch unmittelbar aufeinander folgende Bekleidung des Amtes allerdings schon seit der frühen Republik vor; seit der Verfassungsreform des Diktators Sulla aus dem Jahr 82 v. Chr. war die wiederholte Bekleidung des Konsulats erst nach zehn Jahren erlaubt. Das Iterationsverbot war neben dem Kollegialitäts- und dem Annuitätsprinzip das wichtigste Mittel, eine gefährliche Machtfülle von Amtsträgern zu verhüten.

Insbesondere in der Krise der Republik kam die Iteration wiederholt vor: Bekannteste Beispiele sind Gaius Sempronius Gracchus, der sich in drei Jahren hintereinander zum Volkstribunen wählen lassen wollte, Gaius Marius, der das Konsulat in fünf aufeinanderfolgenden Jahren (104 bis 100 v. Chr) und insgesamt sieben Mal ausübte, sowie Gaius Iulius Caesar, der das Konsulat in den Jahren 59, 48, 46, 45 und 44 v. Chr. bekleidete. In der Kaiserzeit ab Augustus war die Iteration des Konsulats Zeichen für eine herausgehobene soziopolitische Stellung. Unmittelbar aufeinanderfolgende Konsulate gab es nur bei Angehörigen des Kaiserhauses.

Philosophie

Jacques Derrida führte den Begriff in die Sprache der Philosophie ein.^[1] "Iteration" bezeichnet hier die Wiederholung eines Begriffs im philosophischen und gesellschaftlichen Diskurs. Laut Derrida verändert sich mit jeder Wiederholung ("Iteration") eines Begriffs seine Bedeutung, so dass niemals dieselbe Bedeutung reproduziert wird wie beim vorausgehenden Gebrauch des Begriffs. Jede Iteration hat vielmehr eine Variation der Bedeutung zur Folge, die dem ursprünglichen Begriff etwas hinzufügt und ihn bereichert. Eine ursprüngliche Definition von Begriffen, auf die man ihre Bedeutung zurückführen könnte, kann es demnach nicht geben.

1. ↑ Jacques Derrida (1988): "Signatur, Ereignis, Kontext", in: Randgänge der Philosophie. Hg.: Peter Engelmann. Wien: Passagen