Reuleaux-Polygon

Bogenpolygone oder auch Bogenvielecke sind Arten von gleichdicken Figuren. Ihnen liegt jeweils ein Vieleck zugrunde, das so erweitert wird, dass alle Eigenschaften von Gleichdicken erfüllt sind.

Die regelmäßige Variante wird als Reuleaux-Polygon bezeichnet. Sie ist benannt nach dem deutschen Ingenieur und Kinematiker Franz Reuleaux (1829-1905).

Gleichdicke sind Körper oder Figuren konstanter Breite das heißt, dass jeder mögliche Durchmesser denselben Betrag hat.

Bogenvielecken liegt stets ein Vieleck zugrunde, das mehrere Eigenschaften besitzen muss:

• Die Seitenzahl ist ungerade.
• Alle Seiten sind gleich lang.
• Das Vieleck überschlägt sich selbst.
• Für Reuleaux-Gleichdicke gilt zusätzlich, dass die Polygone regelmäßig sein müssen.

Konstruktion

Zuerst verbindet man aus kosmetischen Gründen zwei benachbarte Punkte, damit sich ein neues Vieleck ergibt. Anschließend trägt man über jeder Seite Kreisbögen an, deren Mittelpunkt jeweils auf der gegenüberliegenden Seite liegt.

Bei einem Fünfeck zeichnet man somit fünf Kreisbögen, bei einem Siebeneck sieben, usw.

Auch ohne Vorgabe eines Polygons lässt sich ein Bogenvieleck allein mit dem Zirkel konstruieren. Hier am Beispiel des Bogenpentagons; die Konstruktionsbeschreibung lässt sich jedoch für alle beliebigen Bogenvielecke adaptieren:

1. Man gibt einen Punkt A vor und nimmt diesen als Mittelpunkt für einen Kreis k, auf dem man beliebig den Punkt B festlegt.
2. Man zeichnet einen Kreis i um den Punkt B
3. Man legt einen Punkt C auf dem Kreis l fest und zeichnet darum einen Kreis j.
4. Man legt einen Punkt D auf dem Kreis m fest. D muss gemessen an einer Gerade AB bezüglich C auf der anderen Seite liegen (im Folgenden bezeichnet als "Jenseits"). Um D zeichnet man nun einen Kreis n.
5. Der diesseitige Schnittpunkt der Kreise n und k ergibt den Punkt E. Ein Kreis o um diesen Punkt vervollständigt die Figur und es sollten die Punkte A und D auf dem Kreis o liegen, damit ein korrektes Gleichdick vorliegt.

Das Gleichdick wird nun gebildet aus den Kreisbogenabschnitten der fünf Kreise, die jeweils zwei Punkte verbinden.

Berechnung des Umfangs

Bei regelmäßigen Bogenfünfecken berechnet sich der Umfang auf folgende Art und Weise:

$U = 5\cdot \frac{2\cdot b \cdot \pi }{360^\circ} \cdot \frac{360^\circ}{2\cdot5} = b\cdot\pi$

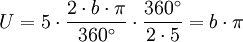
Diese Rechnung lässt sich verallgemeinern auf regelmäßige Bogenvielecke beliebiger, ungerader Eckenzahl:

$U = n\cdot\frac{2\cdot b \cdot \pi}{360^\circ}\cdot\frac{360^\circ}{2 \cdot n} = b \cdot \pi$

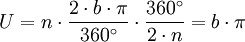
Daraus erkennt man, dass der Umfang beliebiger regelmäßiger Bogenvielecke gleich ist.