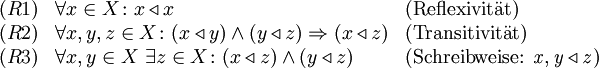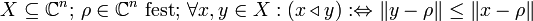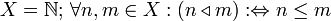Richtung (Mathematik)

In der Mathematik heißt eine nicht-leere Menge X genau dann gerichtete Menge, wenn auf ihr eine Relation "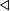$\triangleleft$" (genannt Richtung) erklärt ist, die folgenden Axiomen genügt:

$\begin{array}{lll} (R1)& \forall x \in X\colon x \triangleleft x & (\mathrm{Reflexivit\ddot at}) \\ (R2)& \forall x,y,z \in X\colon (x \triangleleft y) \and (y \triangleleft z) \Rightarrow (x \triangleleft z) & (\mathrm{Transitivit\ddot at}) \\ (R3)& \forall x,y \in X\ \exists z \in X\colon (x \triangleleft z) \and (y \triangleleft z) & (\mbox{Schreibweise: } \mathit{x,y \triangleleft z}) \\ \end{array}$

Um die Richtung hervorzuheben (auf einer Menge können durchaus mehrere Richtungen erklärt sein) nennt man auch das geordnete Paar 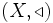$\left(X,\triangleleft \right)$ gerichtete Menge. Sprechweise für 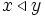$x \triangleleft y$ ist "x vor y" oder auch "y nach x". Unter 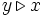$y \triangleright x$ versteht man $x \triangleleft y$.

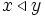Anschauliche Deutung

Das eigentliche Richtungsaxiom ist (R3). Es erlaubt, an jedem Punkt x der Menge X einen weiteren Punkt z zu finden, der "hinter" x liegt, indem man in (R3) y:=x setzt. Damit kann man in X einen "Kurs" einschlagen: Man wähle einen Punkt x₀ aus (ein solcher existiert, da X nicht leer ist). Zu diesem bestimme man durch (R3) mit x=y=x₀ einen Punkt x₁. Zu diesen beiden bestimme man wieder durch (R3) mit x=x₀ und y=x₁ einen Punkt x₂. Analog bestimme man zu x₁ und x₂ einen Punkt x₃, und man erhält induktiv fortfahrend eine Folge 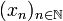$(x_n)_{n\in\mathbb{N}}$ mit $x_0 \triangleleft x_1 \triangleleft x_2 \triangleleft \cdots \triangleleft x_k \triangleleft \cdots$.

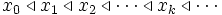Beispiele

• $X \subseteq \mathbb{C}^n; \, \rho \in \mathbb{C}^n\ \mathrm{fest}; \, \forall x,y \in X: (x \triangleleft y) :\Leftrightarrow \left\| y - \rho \right\| \le \left\| x - \rho \right\| \quad$
  

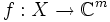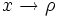(Sprechweise: "X ist auf ρ gerichtet", "ρ ist Richtungszentrum von X") Man kann durch diese Richtung den Grenzwert einer Funktion $f: X \to \mathbb{C}^m$ für $x \to \rho$ als (Netz)Konvergenz des zugehörigen Netzes auffassen.

• $X = \mathbb{N}; \, \forall n,m \in X: (n \triangleleft m) :\Leftrightarrow n \leq m$
  

• $X = \mathbb{R}; \, \forall x,y \in X: (x \triangleleft y) :\Leftrightarrow x \leq y$
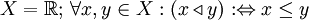
  Mit Hilfe dieser gerichteten Mengen lassen sich Grenzwerte von Funktionen bzw. Folgen für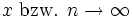 $x \mbox{ bzw. } n \to \infty$, ähnlich dem ersten Beispiel, als (Netz)Konvergenzen ihrer zugehörigen Netze auffassen.

• $X = \mathbb{N}^2; \, \forall (n,m),(p,q) \in X: ((n,m) \triangleleft (p,q)) :\Leftrightarrow (n \leq p) \and (m \leq q)$
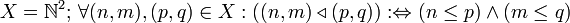
  Mit dieser Richtung auf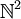 $\mathbb{N}^2$ lässt sich Konvergenz von Doppelfolgen, wiederum als Netzkonvergenz, definieren.

• M eine beliebige nicht-leere Menge und $X = \mathcal{P}(M); \, \forall A, B \in X: (A \triangleleft B) :\Leftrightarrow A \subseteq B$