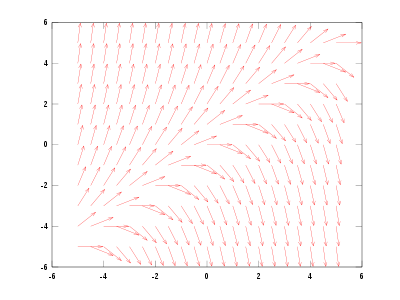
Richtungsfeld

Ein Richtungsfeld dient zur zeichnerischen Bestimmung von Näherungslösungen einer Differentialgleichung.

Mathematische Beschreibung

Ein Richtungsfeld einer (expliziten) Differentialgleichung (erster Ordnung) y'(x) = F(x,y(x)) wird gebildet, indem man jedem Punkt (x,y) in der Ebene einen Vektor mit Steigung F(x,y) zuordnet. Dieser gibt die Richtung an, in der die Graphen möglicher Lösungen der Differentialgleichung, die durch den Punkt (x,y) gehen, verlaufen.

Praktisch heißt das, dass in einem Koordinatensystem beliebige Punkte P(x,y) gewählt werden und dazu die Steigung durch Einsetzen in die Differentialgleichung berechnet wird. (Denn die Ableitung von y, y', entspricht gerade der Steigung der Funktion.)

Zu y'(x) = F(x,y(x)) lautet die Gleichung der einzelnen Tangentenstücke der Länge l:

$\vec{v}(x,y;\lambda)=\begin{pmatrix}x\\ y\end{pmatrix}+\frac{\lambda}{\sqrt{1+F^{2}(x,y)}}\begin{pmatrix}1\\ F(x,y)\end{pmatrix}\quad\text{mit}\quad\lambda=\left[-\frac{l}{2},\frac{l}{2}\right]$

Beispiel

Richtungsfeld für y' = y − x

Die Differentialgleichung y'(x) = y(x) − x besitzt in allen Punkten (C,C) die Steigung 0, da diese gegeben ist durch m = y − x = C − C = 0. Im Punkt P₁(x,y) = (1,2) beträgt sie m = 2 − 1 = 1, im Punkt P₂(x,y) = ( − 4,2) dann m = 2 − ( − 4) = 6. Mit genügend vielen Punkten bekommt man ein Richtungsfeld, in dem mögliche Lösungen zumindest ansatzweise sichtbar werden.

Octave-Script für Richtungsfeld

Das Script für GNU Octave zeichnet ein Richtungsfeld für eine Differentialgleichung ersten Grades.

function Richtungsfeld(dgl)
% dgl ist die erste Ableitung von x nach t und ist i.A. eine Funktion von x und t
 
% Ausschnitt und Abstand zwischen den Vektoren
x = -5:1:5;
t = -5:.5:5;
 
for x_n = 1:length(x)
  for t_n = 1:length(t)
    len = sqrt( dgl(x(x_n), t(t_n))^2 + 1 ); % Länge des Vektors für Normierung
    dt(x_n,t_n) = 1 / len;                   % Länge des Vektors entlang der Abszisse
    dx(x_n,t_n) = dgl(x(x_n), t(t_n)) / len; % Länge des Vektors entlang der Ordinate
  end
end
 
quiver(t, x, dt, dx, 'r');  % Vektoren zeichnen
 
print('field.svg', '-dsvg')  % Plot als svg-Datei exportieren
%print('field.png', '-dpng')  % alternativ als png-Datei

Speichern unter 'Richtungsfeld.m'. Aufruf des Skripts für die Differentialgleichung $\dot{x}(t) = x(t) - t$ wie folgt:

dgl = @(x, t) x-t   % Funktionsdefinition
Richtungsfeld(dgl)  % Aufruf des Skripts

Siehe auch

• Isoklinen: Kurven, die Punkte mit gleicher Steigung verbinden
• Trajektorie (Mathematik)
• Phasenraum
• Vektorfeld

Literatur

• W. Walter: Gewöhnliche Differentialgleichungen: Eine Einführung. 7. Auflage, Springer, Berlin 2000, ISBN 3-540-67642-2
• F. Reinhardt, H. Soeder: dtv-Atlas Mathematik. Band 2, 11. Auflage, Deutscher Taschenbuch Verlag, 1998, ISBN 3-423-03008-9