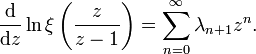- Riemann'sche Xi-Funktion
-
 Die Riemannsche ξ-Funktion in der komplexen Zahlenbene.
Die Riemannsche ξ-Funktion in der komplexen Zahlenbene.In der Mathematik ist die riemannsche Xi-Funktion eine Transformierte der riemannschen Zeta-Funktion. Ihre Nullstellen entsprechen dabei ausschließlich den nichttrivialen Nullstellen der Zeta-Funktion, und im Gegensatz zu dieser ist die Xi-Funktion holomorph auf der ganzen komplexen Ebene. Zudem genügt sie einer besonders einfachen Funktionalgleichung. Bernhard Riemann führte sie 1859 in derselben Arbeit über die Primzahlverteilung ein, in der er auch die später nach ihm benannte riemannsche Vermutung formulierte.
Inhaltsverzeichnis
Definition
Die riemannsche Xi-Funktion ξ ("klein xi") ist definiert als
wo ζ die riemannsche ζ-Funktion und Γ die Gamma-Funktion bezeichnet. Der Produktterm auf der rechten Seite vor der riemannschen ζ-Funktion eliminiert genau alle negativen Nullstellen und die Singularität der Zeta-Funktion. Die Nullstellen von ξ sind daher genau die nichttrivialen Nullstellen der ζ-Funktion.
Eine Variante der Xi-Funktion wird üblicherweise mit Ξ ("groß Xi") bezeichnet und geht aus ξ durch die Variablentransformation
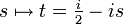 (also
(also 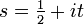 ) hervor:
) hervor:Die riemannsche Vermutung ist äquivalent zu der Aussage, dass alle Nullstellen von Ξ reell sind.
Bemerkenswerterweise verwendete Riemann selber den Buchstaben ξ zur Bezeichnung derjenigen Funktion, die man heute (nach Landau) mit Ξ bezeichnet; die Ursache für diese zunächst verwirrende Symbolik liegt in einem offenbaren Fehler Riemanns[1], der aber keinerlei Auswirkungen auf die Aussagen seines Artikels hat.
Eigenschaften
Spezielle Werte
Es gilt
Für gerade natürliche Zahlen gilt
wobei B2n eine Bernoulli-Zahl bezeichnet. Beispielsweise lauten
Funktionalgleichung
Die Xi-Funktion genügt der Funktionalgleichung ("Reflektionsformel")
- ξ(1 − s) = ξ(s)
oder äquivalent dazu für die Ξ-Funktion:
- Ξ( − t) = Ξ(t)
Ξ ist damit eine gerade Funktion.
Produktdarstellung
wobei ρ in der Produktformel über alle Nullstellen von ξ läuft.[2]
Beziehung zur Riemann-Siegel'schen Z-Funktion
Es gilt[3]
Asymptotisches Verhalten
Für reelle Werte von s gilt[4]
also
(wobei Θ das Landau-Symbol bezeichnet). Entsprechend gilt für reelle Werte von t[5]
Li-Koeffizienten
Die Xi-Funktion ξ hat eine enge Beziehung zu den so-genannten Li-Koeffizienten
denn es gelten die Beziehungen[6]
und
Das lische Kriterium ist die Eigenschaft λn > 0 für alle positiven n. Es ist äquivalent zu der riemannschen Vermutung.
Literatur
- H. M. Edwards: Riemann's Zeta Function. Dover Publications, Mineola, NY 2001, ISBN 0-486-41740-9
- J. C. Lagarias: Li coefficients for automorphic L-functions. 2004. ArXiv: math.MG/0404394
- B. Riemann: Über die Anzahl der Primzahlen unter einer gegebenen Größe. In: Monatsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin. 1859
- E. C. Titchmarsh: The Theory of the Riemann Zeta Function, Second revised (Heath-Brown) edition. Oxford University Press 1986, ISBN 0-19-853369-1
Weblinks
- Eric W. Weisstein: Xi Function auf MathWorld (englisch)
Einzelnachweise
Wikimedia Foundation.

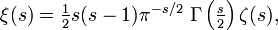
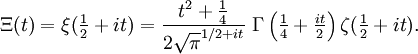
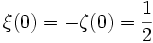
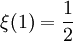
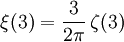
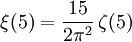
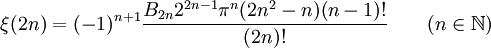
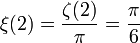
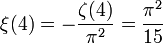
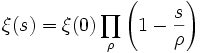
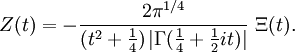
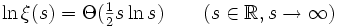
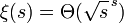
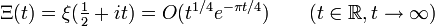
![\lambda_{n} = \sum_\rho \left[ 1 - \left(1-\frac{1}{\rho}\right)^n\right],](/pictures/dewiki/52/4e0943ae76851729e2cc37cab7d36d58.png)
![\lambda_{n} = \frac{1}{(n-1)!}\ \left.\frac{\mathrm{d}^n}{\mathrm{d}s^n}\ [s^{n-1} \ln \xi(s)]\right|_{s=1}
\qquad (n \geqq 1)](/pictures/dewiki/97/a85fed2c852abd1f5450f473e1d145f6.png)