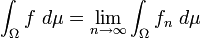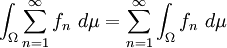Satz von der monotonen Konvergenz — Der Satz von der monotonen Konvergenz, auch Satz von Beppo Levi genannt (nach Beppo Levi), ist ein wichtiger Satz aus der Maß und Integrationstheorie, einem Teilgebiet der Mathematik. Er trifft eine Aussage darüber, unter welchen Voraussetzungen… … Deutsch Wikipedia
Beppo Levi — (* 14. Mai 1875 in Turin, Italien; † 28. August 1961 in Rosario, Argentinien) war ein italienischer Mathematiker. Nach dem Studium an der Universität Turin unter anderem bei Giuseppe Peano und … Deutsch Wikipedia
Integrable Funktion — Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen Maßräumen ermöglicht. Im Fall der reellen Zahlen mit dem Lebesgue Maß stellt das Lebesgue Integral… … Deutsch Wikipedia
Integrierbare Funktion — Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen Maßräumen ermöglicht. Im Fall der reellen Zahlen mit dem Lebesgue Maß stellt das Lebesgue Integral… … Deutsch Wikipedia
Lebesgue-integrierbar — Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen Maßräumen ermöglicht. Im Fall der reellen Zahlen mit dem Lebesgue Maß stellt das Lebesgue Integral… … Deutsch Wikipedia
Lebesgueintegral — Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen Maßräumen ermöglicht. Im Fall der reellen Zahlen mit dem Lebesgue Maß stellt das Lebesgue Integral… … Deutsch Wikipedia
Lebesgue-Integral — Illustration der Grenzwertbildung beim Riemann Integral (blau) und beim Lebesgue Integral (rot) Das Lebesgue Integral (nach Henri Léon Lebesgue) ist der Integralbegriff der modernen Mathematik, der die Berechnung von Integralen in beliebigen… … Deutsch Wikipedia
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
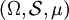 ein Maßraum. Für jede Folge
ein Maßraum. Für jede Folge 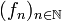 nichtnegativer, messbarer Funktionen
nichtnegativer, messbarer Funktionen 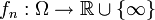 , die μ-fast überall monoton wachsend gegen eine messbare Funktion
, die μ-fast überall monoton wachsend gegen eine messbare Funktion 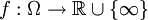 konvergiert, so gilt
konvergiert, so gilt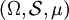 wieder ein Maßraum. Für jede Folge
wieder ein Maßraum. Für jede Folge 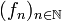 nichtnegativer, messbarer Funktionen
nichtnegativer, messbarer Funktionen 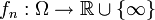 gilt
gilt