- Messbare Funktion
-
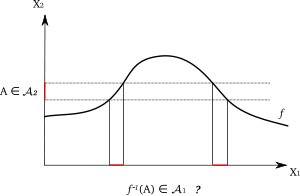
Eine messbare Funktion ist in der Mathematik definiert als eine Funktion f aus einem Messraum
 in einen anderen Messraum
in einen anderen Messraum  , bei der das Urbild jeder messbaren Teilmenge aus X2 eine messbare Teilmenge von X1 ist. Eine solche Funktion wird auch als
, bei der das Urbild jeder messbaren Teilmenge aus X2 eine messbare Teilmenge von X1 ist. Eine solche Funktion wird auch als  -
- -messbar bezeichnet.
-messbar bezeichnet.Inhaltsverzeichnis
Spezialfälle
- Ist der Zielbereich der Funktion ein normierter oder metrischer Raum, so stattet man diesen üblicherweise mit der von diesem erzeugten Borelschen σ-Algebra aus und erwähnt die Algebra nicht weiter, sondern spricht einfach von Messbarkeit.
- Ist der Definitionsbereich der Funktion der
 stattet man diesen üblicherweise mit der σ-Algebra der Lebesgue-messbaren Mengen aus.
stattet man diesen üblicherweise mit der σ-Algebra der Lebesgue-messbaren Mengen aus.
- Eine Funktion
 erfüllt beide obigen Bedingungen. Sie ist entsprechend messbar, wenn das Urbild von Borelmengen eine Lebesgue-messbare Menge ist.
erfüllt beide obigen Bedingungen. Sie ist entsprechend messbar, wenn das Urbild von Borelmengen eine Lebesgue-messbare Menge ist.
Einordnung
Der Begriff der Messbarkeit wird durch die Definition der Integration von Henri Lebesgue motiviert: Für die Lebesgue-Integration einer Funktion
 bezüglich des Lebesgue-Maßes muss Mengen der Form f − 1([a,b]) ein Maß zugeordnet sein. Beispiele für Funktionen, für die dies nicht möglich ist, sind Indikatorfunktionen von Vitali-Mengen. Die Definition der Lebesgue-Integration für beliebige Maßräume führt dann zu obiger Definition der messbaren Funktion.
bezüglich des Lebesgue-Maßes muss Mengen der Form f − 1([a,b]) ein Maß zugeordnet sein. Beispiele für Funktionen, für die dies nicht möglich ist, sind Indikatorfunktionen von Vitali-Mengen. Die Definition der Lebesgue-Integration für beliebige Maßräume führt dann zu obiger Definition der messbaren Funktion.Der Begriff der messbaren Funktion hat Parallelen zur Definition der stetigen Funktion. Eine Funktion zwischen topologischen Räumen X1 und X2 ist stetig, wenn die Urbilder offener Mengen von X2 wiederum offene Mengen von X1 sind. Die von den offenen Mengen erzeugte σ-Algebra ist die borelsche σ-Algebra. Eine stetige Funktion ist also messbar bezüglich der Borel-σ-Algebren von X1 und X2, kurz borel-messbar. Eine gewisse Umkehrung dieser Aussage ist der Satz von Lusin.
Messbare Funktionen spielen als Zufallsvariablen eine wichtige Rolle in der Wahrscheinlichkeitstheorie.
Eigenschaften
Indikatorfunktionen von messbaren Mengen und Linearkombinationen solcher Funktionen (sogenannte einfache Funktionen) sind Beispiele messbarer Funktionen von einem Maßraum in die reellen Zahlen, ausgestattet mit der Borel-σ-Algebra.
Die Verkettung messbarer Funktionen ist wieder eine messbare Funktion, genauer: ist f
 -
- -messbar und g
-messbar und g  -
- -messbar, so ist g o f
-messbar, so ist g o f  -
- -messbar.
-messbar.Eine (reelle) Lebesgue-Borel-messbare Funktion ist nicht unbedingt Borel-Borel-messbar. Auch ist eine Lebesgue-Borel-messbare Funktion nicht unbedingt Lebesgue-Lebesgue-messbar. Die Verkettung zweier Lebesgue-Borel-messbarer Funktionen ist also nicht zwangsläufig wiederum Lebesgue-Borel-messbar. [1] [2]
Starke Messbarkeit
Ist eine Funktion in einen metrischen Raum punktweiser Limes von Elementarfunktionen, d.h. messbaren Funktionen mit endlichem Bild, so heißt sie „stark messbar“.
- Jede messbare Funktion mit separablem Bild ist stark messbar.
- Jede stark messbare Funktion ist messbar.
Starke Messbarkeit und Messbarkeit unterscheiden sich nur voneinander, wenn der Zielraum nicht-separabel ist. Dies ist beispielsweise bei der Definition von verallgemeinerten Integralen wie dem Bochner-Integral der Fall.
Prüfung der Messbarkeit auf Erzeugendensystem
Werden die σ-Algebren
 von den Mengen
von den Mengen  und
und  erzeugt; also
erzeugt; also  , dann genügt es, die Messbarkeit von f für alle
, dann genügt es, die Messbarkeit von f für alle  zu zeigen.
zu zeigen.Für eine Abbildung f von einem Messraum
 nach
nach  gilt somit, dass f genau dann messbar ist, wenn eines der Mengensysteme
gilt somit, dass f genau dann messbar ist, wenn eines der Mengensysteme ,
, ,
, ,
,
in
 liegt (wenn als σ-Algebra auf
liegt (wenn als σ-Algebra auf  die Borelsche σ-Algebra genommen wird). Dabei ist
die Borelsche σ-Algebra genommen wird). Dabei ist  etc. als Abkürzung für
etc. als Abkürzung für ![\{x\in X | f(x)\leq a\}=f^{-1}((-\infty,a])](2/6e27935db5b587668d7a7cd770a0c1cb.png) zu verstehen. Es würde auch ausreichen, wenn das a nur alle rationalen Zahlen durchläuft.
zu verstehen. Es würde auch ausreichen, wenn das a nur alle rationalen Zahlen durchläuft.Abgrenzung
Eine Teilmenge eines Messraums heißt messbar, wenn sie Element der σ-Algebra des Messraums ist und ihr somit ein Maß zugeordnet werden kann.
Literatur
- Jürgen Elstrodt: Maß- und Integrationstheorie. 4. Auflage, Springer, Berlin 2005, ISBN 3-540-21390-2.
- Henri Lebesgue: Leçons sur l'intégration et la recherche des fonctions primitives. Gauthier-Villars, Paris 1904.
Einzelnachweise
- ↑ Robert B. Ash, Catherine Doléans-Dade: Probability and measure theory. Academic Press, 2000, ISBN 0120652021. S. 41.
- ↑ Vladimir Igorevich Bogachev: Measure theory. Springer, 2007, ISBN 3540345132. S. 193.
Wikimedia Foundation.