- Satz von Borelli
-
Das Borel-Cantelli-Lemma (nach Émile Borel und Francesco Cantelli) ist ein Satz der Wahrscheinlichkeitstheorie. Es ist oftmals sehr hilfreich bei der Untersuchung auf fast sichere Konvergenz von Zufallsvariablen.
Es sei
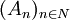 eine unendliche Folge zufälliger Ereignisse. Dann besagt das Borel-Cantelli-Lemma:
eine unendliche Folge zufälliger Ereignisse. Dann besagt das Borel-Cantelli-Lemma:Ist die Summe der Wahrscheinlichkeiten der An endlich, so ist die Wahrscheinlichkeit des limes superior der An gleich 0. Dies ist der „klassische“ Satz von Borel-Cantelli.
Ist die Summe der Wahrscheinlichkeiten der An unendlich und sind die Ereignisse An wenigstens paarweise unabhängig, so ist die Wahrscheinlichkeit des limes superior der An gleich 1. Diese Erweiterung stammt von Paul Erdős und Alfréd Rényi.
Symbolisch: Für
gilt:
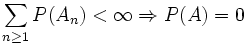
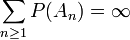 und die An sind paarweise unabhängig
und die An sind paarweise unabhängig 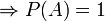
Beweis:
Veranschaulichung am Beispiel:Betrachte die Dualzahldarstellung einer beliebigen reellen Zahl zwischen 0 und 1. Diese Darstellung besteht nur aus Nullen und Einsen. Wählt man eine beliebige reelle Zahl aus, dann kann jede Ziffer entweder Null oder Eins sein. Wir können nun den Wert für jede Ziffer als Zufallsvariable auffassen, deren Wert entweder 1 oder 0 ist. Das in der Definition gegebene An ist also 1 oder 0, wobei n die n-te Nachkommastelle beschreibt.
Wir fragen nun nach der Wahrscheinlichkeit, dass in der Dualzahldarstellung einer beliebigen reellen Zahl unendlich viele Einsen vorkommen, oder anders ausgedrückt, dass das Ereignis An = 1 unendlich oft vorkommt. Es ist intuitiv klar, dass die Wahrscheinlichkeit für 0 oder 1 für jede Ziffer gleich groß ist, wenn die ausgewählte Zahl wirklich beliebig ist, d.h.
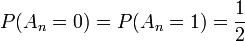
für alle n. Damit ist
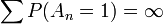 und nach dem Lemma von Borel-Cantelli folgt somit, dass P(A) = 1, wobei A bedeutet, dass unendlich viele Einsen vorkommen. Damit ist gezeigt, dass die Dualzahldarstellung einer beliebigen reellen Zahl (zwischen 0 und 1, aber das lässt sich selbstverständlich auf alle reellen Zahlen ausdehnen) fast sicher unendlich viele Einsen enthält. Analog gilt dies auch für Nullen. Somit ist die Menge der Zahlen, die nur endlich viele Einsen oder Nullen enthalten, eine Nullmenge.
und nach dem Lemma von Borel-Cantelli folgt somit, dass P(A) = 1, wobei A bedeutet, dass unendlich viele Einsen vorkommen. Damit ist gezeigt, dass die Dualzahldarstellung einer beliebigen reellen Zahl (zwischen 0 und 1, aber das lässt sich selbstverständlich auf alle reellen Zahlen ausdehnen) fast sicher unendlich viele Einsen enthält. Analog gilt dies auch für Nullen. Somit ist die Menge der Zahlen, die nur endlich viele Einsen oder Nullen enthalten, eine Nullmenge. -
Wikimedia Foundation.

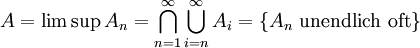
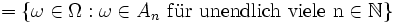
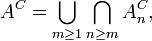
![\begin{align}
P \left( A^C \right)
&\le \sum_{m \ge 1} P \left( \bigcap_{n \ge m} A_n^C \right)\\
&= \sum_{m \ge 1} \lim_{l \to \infty} P \left( \bigcap_{n = m}^l A_n^C \right)\\
&= \sum_{m \ge 1} \lim_{l \to \infty} \left[ \prod_{n=m}^l 1-P \left(A_n\right) \right]\\
&\le \sum_{m \ge 1} \lim_{l \to \infty} \exp \left[- \sum_{n=m}^l P \left(A_n\right) \right]\\
&= \sum_{m \ge 1} 0\\
&= 0.
\end{align}](/pictures/dewiki/56/8e454137d8ae78f9daee5c70ddab9a42.png)