Satz von Kuratowski

Der Satz von Kuratowski (nach Kazimierz Kuratowski) ist ein Satz aus der Graphentheorie, der wichtige Aussagen zu planaren Graphen macht und die Frage nach der Planarität (Plättbarkeit) eines Graphen beantwortet.

Planarität

Allgemein formuliert ist ein Graph genau dann planar (plättbar), wenn es möglich ist, den Graphen so in die Ebene zu zeichnen, dass sich die Kanten des Graphen nicht schneiden. Die Kanten dürfen sich lediglich in den Knoten des Graphen berühren.

Die folgenden beiden Graphen sind planar, wobei die Planarität von G2 erst deutlich wird, wenn man G2 anders zeichnet.

Abb. 1: Beispielgraphen G1 und G2

Die Graphen K_3,3 und K₅

Abb. 2: K₅

Abb. 3: K_3,3

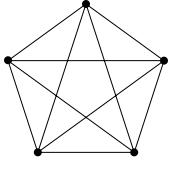
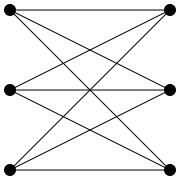
Der Satz von Kuratowski benutzt zwei spezielle Graphen: K₅ und K_3,3. Bei K₅ handelt es sich um den vollständigen Graphen mit 5 Knoten (siehe Abb. 2), bei K_3,3 um einen vollständig bipartiten Graphen, der in zwei je dreielementige Teilmengen aufgeteilt ist (siehe Abb. 3). Beide Graphen sind nicht planar. Sie sind sogar die kleinsten nicht-planaren Graphen überhaupt, was direkt aus dem Satz von Kuratowski folgt.

Der Satz von Kuratowski

Ein endlicher Graph ist genau dann planar, wenn er keinen Teilgraphen enthält, der durch Unterteilung von K₅ oder K_3,3 entstanden ist.

Unterteilung bedeutet hier das beliebig oft wiederholbare (auch nullmalige) Einfügen von neuen Knoten auf Kanten. Mit Teilgraph ist hier ein Graph gemeint, der aus dem ursprünglichen Graphen durch Entfernen von Knoten bzw. Kanten entsteht.

Eine äquivalente Formulierung des Satzes von Kuratowski ist:

Ein Graph G ist genau dann planar, wenn er keinen zu K₅ oder K_3,3 homöomorphen Teilgraphen enthält.

Eine Variante ist der Satz von Wagner:

Ein Graph G ist genau dann planar, wenn weder K₅ noch K_3,3 ein Minor von G ist.

Literatur

• Casimir Kuratowski: Sur le problème des courbes gauches en topologie. In: Fund. Math. 15. 1930, 271-283.